Maths - Conversion Matrix to Axis Angle

key:

• + means a positive value
• - means a negative value
• 0 means very close to zero (within epsilon)

where two sets of values give the same result they are shown on the same line for instance:

means x and y have same sign and z has opposite sign.

Note we can only distinguish 4 non-zero combinations from x*y , x*z and y*z, for instance +x,+y,+z gives the same matrix as -x,-y,-z this is because rotation by +180 degrees produces exactly the same rotation as -180° and we don't know which way it went round unless we happen to know any intermediate values.

Where we have to be careful is when x, y or z are close to zero and so a small error might flip between + and -. If x*y , x*z and y*z are all zero then we are rotating purely about one axis, the sign in this case is not important. If one of them is zero then we may have to invert one of the others as shown in the table above.

So the algorithm emerging is as follows:

 if (matrix symmetrical) {
   if (identity matrix) return zero angle
   // this is 180 deg rotation
   calculate axis with positive values
   if (x is zero and y,z are not zero) invert y or z
   else if (y is zero and z is not zero) invert x or z
   else if (z is zero) invert x or y
   else if (x*y , x*z and y*z are all positive) return positive values
   else if (y*z is positive) invert x
   else if (x*z is positive) invert y
   else if (x*y is positive) invert z
}

Java Code

/**
This requires a pure rotation matrix 'm' as input.
*/
public axisAngle toAxisAngle(matrix m) {
  double angle,x,y,z; // variables for result
	double epsilon = 0.01; // margin to allow for rounding errors
	// optional check that input is pure rotation, 'isRotationMatrix' is defined here:
	// http://www.euclideanspace.com/maths/algebra/matrix/orthogonal/rotation/
	assert isRotationMatrix(m) : "not valid rotation matrix" ;// check during debugging only
	if ((Math.abs(m[0][1]-m[1][0])< epsilon)
	  && (Math.abs(m[0][2]-m[2][0])< epsilon)
	  && (Math.abs(m[1][2]-m[2][1])< epsilon)) {
		// singularity found
		// first check for identity matrix which must have +1 for all terms in leading diagonal
		// and zero in other terms
		if ((Math.abs(m[0][1]+m[1][0]) < 0.1)
		  && (Math.abs(m[0][2]+m[2][0]) < 0.1)
		  && (Math.abs(m[1][2]+m[2][1]) < 0.1)
		  && (Math.abs(m[0][0]+m[1][1]+m[2][2])-3) < 0.1) {
			// this singularity is identity matrix so angle = 0
			// note epsilon is greater in this case since we only have to distinguish between 0 and 180 degrees
			return new axisAngle(0,1,0,0); // zero angle, arbitrary axis
		}
		// otherwise this singularity is angle = 180
		angle = Math.PI;
		x = (m[0][0]+1)/2;
		if (x > 0) { // can only take square root of positive number, always true for orthogonal matrix
			x = Math.sqrt(x);
		} else {
			x = 0; // in case matrix has become de-orthogonalised
		}
		y = (m[1][1]+1)/2;
		if (y > 0) { // can only take square root of positive number, always true for orthogonal matrix
			y = Math.sqrt(y);
		} else {
			y = 0; // in case matrix has become de-orthogonalised
		}
		z = (m[2][2]+1)/2;
		if (z > 0) { // can only take square root of positive number, always true for orthogonal matrix
			z = Math.sqrt(z);
		} else {
			z = 0; // in case matrix has become de-orthogonalised
		}
		boolean xZero = (Math.abs(x)<epsilon);
		boolean yZero = (Math.abs(y)<epsilon);
		boolean zZero = (Math.abs(z)<epsilon);
		boolean xyPositive = (m[0][1] > 0);
		boolean xzPositive = (m[0][2] > 0);
		boolean yzPositive = (m[1][2] > 0);
		if (xZero && !yZero && !zZero) { // implements  last 6 rows of above table
		  if (!yzPositive) y = -y;
		} else if (yZero && !zZero) {
		  if (!xzPositive) z = -z;
		} else if (zZero) {
		  if (!xyPositive) x = -x;
		}
		return new axisAngle(angle,x,y,z);
	}
	double s = Math.sqrt((m[2][1] - m[1][2])*(m[2][1] - m[1][2])+(m[0][2] - m[2][0])*(m[0][2] - m[2][0])+(m[1][0] - m[0][1])*(m[1][0] - m[0][1])); // used to normalise
	if (Math.abs(s) < 0.001) s=1; // prevent divide by zero, should not happen if matrix is orthogonal and should be
		// caught by singularity test above, but I've left it in just in case
	angle = Math.acos(( m[0][0] + m[1][1] + m[2][2] - 1)/2);
	x = (m[2][1] - m[1][2])/s;
	y = (m[0][2] - m[2][0])/s;
	z = (m[1][0] - m[0][1])/s;
   return new axisAngle(angle,x,y,z);
}

thanks to Vladimir Smutny for the correction and Andreas Keil here.

Issues

• For issues concerning acos see here.
• Most trig functions (except openGL) use radians not degrees.

Another Example

we take the 90 degree rotation from this:

to this: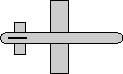

As shown here the matrix for this rotation is:

So using the above result:

angle = acos ( ( m00 + m11 + m22 - 1)/2) = acos (0) = 90 degrees
x = (m21 - m12)/sqrt((m21 - m12)²+(m02 - m20)²+(m10 - m01)²) = 2 / sqrt (4) = 1
y = (m02 - m20)/sqrt((m21 - m12)²+(m02 - m20)²+(m10 - m01)²) = 0
z = (m10 - m01)/sqrt((m21 - m12)²+(m02 - m20)²+(m10 - m01)²) = 0

angle = 90°
axis = 1,0,0

As you can see here, this gives the result that we are looking for.

Angle Calculator and Further examples

I have put a java applet here which allows the values to be entered and the converted values shown along with a graphical representation of the orientation.

Also further examples in 90° steps here