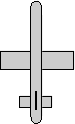
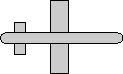
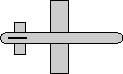
When we are modelling rotation it is important to consider the frame of reference. In the following we will use the example of an aeroplane, to a person on the ground the aeroplane might be turning right, but to a person in the aeroplane the ground will appear to be turning left. So the orientation of the plane relative to the ground is minus the orientation of the ground relative to the plane.
But the situation gets more complicated when we are trying to work out the result of a sequence of rotations, I can think of two possible ways to combine two rotations. In the first case we used the fixed global co-ordinates for everything, in the second case we specify the second rotation in the local co-ordinates of the aeroplane, which have been rotated by the first rotation.
Note: the following assumes:
- A rectangular (Cartesian) co-ordinate system.
- A right hand convention for direction of rotations.
The following examples show two possible ways to combine rotations:
Global frame-of-reference
always defines rotations in global coordinates, in this case x=right, y=up, z=toward viewer. In this case the matrix or quaternion representations of the individual rotations can be combined by multipling in the following order:
[resulting transform] = [second transform] * [first rotation]
To see why this is we could multiply vector Vin by matrix [A] to produce an intermediate vector Vmid, we then multipy this by matrix [B]. If we sustitute [A]Vin for Vmid we can see that the overall matrix = [B][A].
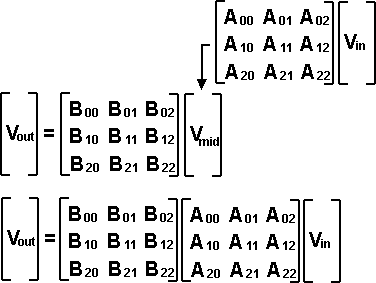
Local frame-of-reference
Defines rotations relative to local coordinates, in other words the coordinate system rotates with the object. In this case the matrix or quaternion representations of the individual rotations can be combined by multipling in the following order:
[resulting transform] = [first rotation] * [second transform]
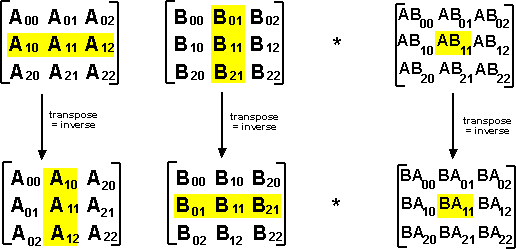
The easiest way to work in this situation is, instead of imagining ourselves looking at the object from outside and calculating its coodinates, instead we imagine ourselves sitting on the object and measure the coordinates of external points. This means that instead of working in terms of the objects position transform, we are working in terms of its inverse (which is the transpose for rotations as explained here). We can now calculate the result of consecutive transforms by multipling the individual transforms as we did before. Normally when we multiply two matricies, we calculate an element by combinig the corresponding row in the first matrix by the corresponding column in the second matrix. However since the matricies are transposed this is equivilant to reversing the order of matricies from the global case. This forms an isomorphism as shown here:
Which to use
The Global frame of reference is easiest for us to understand and it makes sense when we are moving objects by hand one step at a time. However, for real world objects, such as aeroplane or a robot arm the first rotation tends to alter the coordinate reference for susequent rotations. Therefore the local frame of reference might be used more often.