Maths - Trigonometry - Inverse trig functions

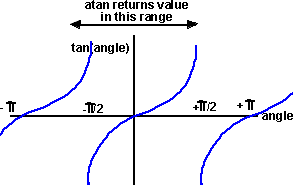
The inverse of the sine function is known as arc sine, most math libraries shorten this to asin

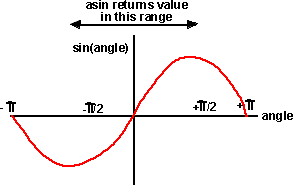
The inverse of the cosine function is known as arc cosine, most math libraries shorten this to acos

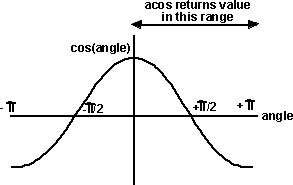
The inverse of the tangent function is known as arc tangent, most math libraries shorten this to atan or atan2

The trig functions are many to one, therefore the inverse trig functions have many possible results. We usually assume that:
acos returns the angle between 0 and pi
asin returns the angle between -pi/2 and pi/2
atan returns the angle between -pi/2 and pi/2
atan2 returns the angle between -pi and pi

Which value to use?

As we can see from the above graphs, trig functions are many to one. That is, for a given value, it could be produced by many angles. In fact since the graph repeats every 2 pi (360 degrees) there are an infinite number of angles. The values returned by the inverse trig functions are shown above. Usually we want the smallest angle that will represent the required rotation.

Rectangular To Polar using atan function

For information about polar coordinates see here.

If we want to convert the rectangular coordinates x,y to the polar coordinates θ,r then we can do so as follows:

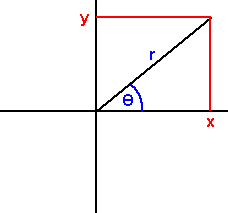
We can calculate r from:

r² = x² + y²

and θ from:

tan(θ) = y / x

which gives:

θ = atan(y / x)

Rectangular To Polar using atan2 function

There are some potential problems with the above approach:

• It does not work for a full range of angles from 0° to 360°, only angles between -90° and +90° will be returned, other angles will be 180° out of phase. For example: the point x=-1,y=-1 will produce the same angle as x=1,y=1 but the above diagram shows that these are in different quadrants.
• points on the vertical axis have x=0, so when we calculate the intermediate result y/x we will get infinity which will generate an exception when calculated on the computer.

Most maths libraries have a atan2(y,x) function which takes both x and y as operands, which allows it to get round the above problems.

In the first quadrant atan2(y,x) is equivalent to atan(y/x) since:

tan(a) = sin(a)/cos(a) = opposite/adjacent = y/x 
and 
atan2(y,x) = atan2(opposite,adjacent)

Most maths libraries, for example java, define the order of operands as: atan2(y,x) but some, for example Excel spreadsheet reverse the order of the operands as follows: 
 
ATAN2(x_num,y_num) 
 
X_num is the x-coordinate of the point. 
 
Y_num is the y-coordinate of the point.

Therefore you should always check the order of the order of operands for the maths library you are using.

package angles;import java.lang.Math;public class Application1 { public static void value(float x,float y) {
   try {
   	System.out.println("x="+x+" y="+y+" atan(y/x)="+Math.atan(y/x)+"    atan2(y,x)="+Math.atan2(y,x));
   } catch (Exception e) {
   	System.out.println("x="+x+" y="+y+" atan(y/x)=error"+"    atan2(y,x)="+Math.atan2(y,x));
   }
 } //Main method
   public static void main(String[] args) {
   value(1,0);
   value(1,1);
   value(0,1);
   value(-1,1);
   value(-1,0);
   value(-1,-1);
   value(0,-1);
   value(1,-1);
   }
   }

EuclideanSpace

home

Problem Solving

Example Dish Example