Maths - Transforms Using Matrices

There are two types of algebra associated with transformations and these algebras must interwork correctly together.

• The first type of algebra defines how a given point is transformed, that is, a given rotation must define where every point, before the rotation, ends up after the rotation.
• The second type of algebra defines how rotations can be combined, that is, we first do 'rotation 1' then we do 'rotation 2' this must be equivalent to some combined rotation, say: 'rotation 3'.

The diagram on the left tries to illustrate this. The blue arrows, going from left to right, show different rotations which take a point Pin and moves it to point Pout. The red arrow, from top to bottom, takes two rotations and combines them to give a third.

Multiply Matrix by Vector

A matrix can convert a vector into another vector by multiplying it by a matrix as follows:

v_out0 v_out1 v_out2

=

m00 m01 m02 m10 m11 m12 m20 m21 m22

v_in0 v_in1 v_in2

We can think of this as transforming

v_in0 v_in1 v_in2

into

v_out0 v_out1 v_out2

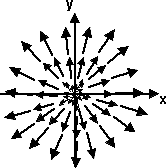
If we apply this to every point in the 3D space we can think of the matrix as transforming the whole vector field.

This can represent any linear transform, including scaling and rotation (translation can be done by adding vectors).

Applying the Transform

The result of this multiplication can be calculated by treating the vector as a n x 1 matrix, so in this case we multiply a 3x3 matrix by a 3x1 matrix we get:

v_out0 v_out1 v_out2

=

m00*v_in0 + m01*v_in1 + m02*v_in2 m10*v_in0 + m11*v_in1 + m12*v_in2 m20*v_in0 + m21*v_in1 + m22*v_in2

So any vector v_in can be converted into another vector v_out.

We can show all vectors as a vector field as shown here.

Scaling

We can scale using the following matrix:

m00	0	0
0	m11	0
0	0	m22

If we want to scale equally in all dimensions then m₀₀ =m₁₁=m₂₂

Translation

We can translate a vector by adding an offset vector, not a linear transform as shown above. Sometimes we want to combine translation with rotation so that we can do both in one operation, but we cant do 3D translation by multiplication with a 3x3 matrix . but we can with a 4x4 matrix as defined here.

Rotation

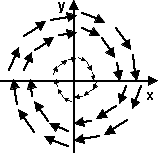
We can use a 3x3 matrix to represent rotation in 3 dimensions as defined here. Rotations in any arbitrary number of dimensions are discussed in group theory.

Sample 3D Rotations

In order to try to explain things I thought it might help to work out a simple case where rotations are only allowed in multiples of 90 degrees. This should make it easier to illustrate the orientation with a simple aeroplane figure, we can rotate this either about the x,y or z axis as shown here:

Properties of rotation matrix

Determinant of Rotation Matrix

det[R] = 1

The determinant (as defined on this page) is plus one (rotation combined with a reflection gives a determinant of minus one).

Eigenvector and Eigenvalues of Rotation Matrix

The eigenvector and eigenvalues (as defined on this page) can best be written in terms of the matrix when it is written in terms of the axis angle representation:

[R] =

t*x*x + c t*x*y - z*s t*x*z + y*s t*x*y + z*s t*y*y + c t*y*z - x*s t*x*z - y*s t*y*z + x*s t*z*z + c

where,

• c =cos(θ)
• s = sin(θ)
• t =1 - c
• x = normalised axis x coordinate
• y = normalised axis y coordinate
• z = normalised axis z coordinate

this gives:

eigenvalues = {1 , e^±iθ} = {1 , cos(θ) ± i sin(θ)}

eigenvector = [x,y,z]

EuclideanSpace

home

Prerequisites

You may want to review vectors:

• Vectors

Transforms

Rotating a Cube

Linear Functions