Abstract
On this page we start by trying to catergorise all possible transformations. One of the most important is an isometry, which is a combination of a translation and a rotation, this is important for mechanics because it can represent all possible movements of a solid body. We therefore go on to discuss the properties of isometries in more detail.
3D Transformations
These transformations map each point in 3D space to a potentially different point in 3D space.
We can build up many types of transformation by using a combination of these simple transforms:
| example | type |
|---|---|
 |
Original |
 |
Translate |
 |
Rotate |
 |
Reflect |
 |
Shear |
 |
Scale |
In some situations we need to need to restrict the types of transformation that are allowed, for example if we are modeling a solid object, it can move and rotate but we might not want it to scale, shear or reflect.
| translation | rotation (around origin) | reflection | glides | scale (from origin) contraction and expansion |
shear | dilation | spiral similarities | |
|---|---|---|---|---|---|---|---|---|
| "proper" Orthogonal | no | yes | no | no | no | no | no | no |
| "improper" Orthogonal | no | yes | yes | no | no | no | no | no |
| "proper" isometries | yes | yes | no | no | no | no | no | no |
| "improper" isometries | yes | yes | yes | yes | no | no | no | no |
| affine (affinity) | yes | yes | yes | yes | yes | yes | yes | yes |
| linear | yes | yes | yes | yes | yes | yes | yes | yes |
| Projective transformations | ||||||||
Isometry
There are 2 types of transformations that can be applied to solid objects without distorting their shapes:
- Translations
- Rotaions
There is another special case which is reflections, although solid objects cant turn into mirror image of them selves we may want to model reflections. For now we will concentrate on translations and reflections.
In 3 dimensions, for solid objects, there are 3 degrees of freedom associated with translation and 3 degrees of freedom associated with rotation. So unconstrained solid objects have 6 degrees of freedom (often denoted 6 DOF objects). In a two dimensional plane, shapes can be translated with 2 degrees of freedom and there is 1 degree of freedom for rotation, so unconstrained 2D shapes have 3 DOF (Degrees of freedom). In one dimension rotation does not apply, so an unconstrained point on a line has one DOF. In higher than 3 dimensions things get a bit more complicated as discussed on this page.
So rotation is independent of translation and can be calculated and combined independently. However a mechanical system is often constrained so that its rotation depends on its translation and visa versa. For example, a jointed system (see this page) such as a hinge, creates constraints that relate translation and rotation.
We don't even need a mechanism to connect rotation and translation, sometimes it seems to arise out of pure geometry, consider a solid body free to rotate around its centre of mass and also free to move in a linear way so that it has 6 DOF. Now consider a subset of this solid body, offset from the centre of mass, its rotation will be the same as the whole body but its translation will depend on both the translation and the rotation. Another example is rotation around a point other than the origin.
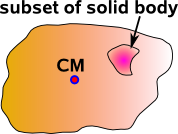 |
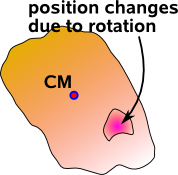 |
In situations like these where we need to calculate the position of particles from a sequence of both translations and rotations it is useful to compose them into a composite transform that represents rotations and transforms in any sequence. A useful algebra for representing such transforms is 4×4 matrix algebra as described on this page. The theoretical underpinnings of this come from projective space, this embeds 3D euclidean space into a 4D space. An alternative algebra we can use for this is 5D geometric algebra. The theoretical underpinnings for this come from conformal space where we can embed a 3D Euclidean space in 5D.
Although it may appear to make things more complicated by moving to higher dimensional spaces, the individual operations become simpler allowing combined translations and rotations to be applied in a single operation. There are also lots of other advantages because it allows us to make an explicit distinction between vectors and points and it allows us to operate on lines, planes, etc. that don't necessarily go through the origin.
see group of spatial displacements SE(n)
This group represents the valid transforms for a solid body. This are known as isometries and they have the properties that:
- They preserve distances in the solid body (they do not change its shape)
- They preserve right or left handedness (they do not allow reflections)
Therefore SE(n) allows both translations and rotations but does not allow reflections, scaling, shears, etc.
Isometry in 2 dimensions SE(2)
Imagine that we want to transform the solid body at 'A' into the solid body at 'B'
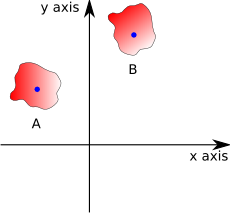
Then we can define a point on A (such as the centre-of-mass) and the corresponding point on B. We can then combine two transforms:
- Do a linear translation such that the point on 'A' is transformed to the point on 'B'.
- Do a rotation about the point so that the solid body is correctly transformed.
However, there is a second option, we can do the translation all in one rotation:
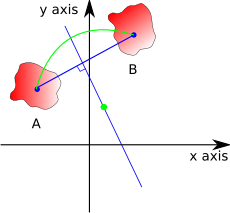
So, provided that we can find a suitable point to rotate around (in the above example shown as green point) we can do the translation and rotation in one operation. The point that we rotate around must by equidistant to the chosen point on each body, therefore it must lie on a line perpendicular to the line joining the two points. So is there always a point that we can find that will do any combination of translation and rotation? To find out we can take two extremes:
- If the rotation point is exactly in the middle of the two objects then the object will be rotated by 180 degrees.
- If the rotating point is at infinity along the bisecting line then the object is translated only and the rotation will be zero.
By putting the point at some distance between these we can get any rotation between 0 and 180 degrees. We can get negative angles by moving in the opposite direction along the line.
Therefore we can do any rotation, translation combination in one rotation.
Doing the rotation-translation in one operation like this can make some calculations simpler and we don't have to consider whether we do the rotation around its original position first and then the translation, or do the translation first and then the rotation about its final position, or do a translation to the mid point first, then the rotation about the mid position and then the final half translation.
For more information about 2D translations and rotations see this page.
Isometry in 3 dimensions SE(3)
In 3 dimensions we can also represent an isometry as a rotation and a translation. Can we represent any isometry as a single rotation as we can in the 2D case as explained above?
In three dimensions there are three degrees of freedom of rotation but when we look for points that are equidistant to the centres of the objects pre and post transform position. The equidistant points lie on a plane which only has two degrees of freedom, but there is also the possibility to rotate around the line from the point. Therefore there are enough degrees of freedom to represent all possible isometrys. However this has not yet proved that we can represent any 3D isometry by a single rotation, can anyone help me with this?
There is another way to represent all possible isometries in three dimensions as a single operation, even though the operation is not a rotation, the operation is represented by a line round the outside of a cylinder. This is known as a screw (see this page for more information).
Choice of algebras for Isometry Transformations
When working on computer graphics, solid body mechanics and related subjects we often need to calculate translations and rotations. It is possible to use separate equations for the translation and the rotation. Translations are relatively simple and can be done using vector addition. However, the two are linked and it would help to have one equation to represent the combined translation in one single operation.
Upto now we have done rotational calculations using either 3 by 3 matrices or quaternions, these algebras can't handle isometry operations but they can be extended to do so:
We can extend 3x3 matrices to 4x4 matrices to allow them to represent translations in addition to rotations.
Or we can extend quaternions to dual quaternions to allow them to represent translations in addition to rotations.
| Pure Rotation (Orthogonal Transform) | 3x3 matrix | quaternion |
| Rotation and Translation (Isometry Transform) | 4x4 matrix | dual quaternion |
Shear (skew) Transform Matrix
The shear transform has the following characteristics:
- determinant = 1
- trace = dimension
for example the two dimensional matrix
| a | b |
| c | d |
we have:
a+d=2
ad-bc=1
An example of a shear (also known as skew) transform is the Galilean transform which allows us to transform between two frames of reference (in classical mechanics) which are moving at a constant velocity relative to each other:
|
is transformed to: |
|
so the transform is:
|
= |
|
|
where:
- vx,vy,vz= relative velocity of the two reference frames in x,y and z directions.
- x,y,z= position in original frame.
- x',y',z'= position in transformed frame.
This assumes time is absolute but distance is skewed:
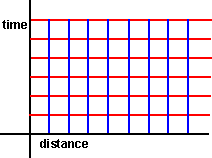 |
—» | 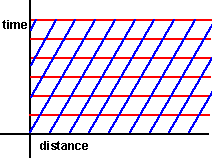 |
More about the Galilean transform.
Affine transformation
An affine transformation is any transformation that preserves collinearity (i.e., all points lying on a line initially still lie on a line after transformation) and ratios of distances (e.g., the midpoint of a line segment remains the midpoint after transformation).
In general, an affine transformation is a composition of rotations, translations, dilations, and shears.
Projective transformations
Projective transformations do not move any objects from the affine space R3 to the plane at infinity or conversely.
Orthogonal transform
can represent rotations only (positive determinant) or rotation and reflection.
Affine transform
can represent translations, rotations, scaling (may be different in x,y and z dimensions), shearing and reflections. Lines remain straight and parallel lines remain parallel, but the angle between intersecting lines can change.
Euclidean transformations
transformations preserve both angles and lengths (i.e. translations, rotations and reflections). Determinant negative if there is a reflection.
Rigid transformation
transformation which can represent the movement of a solid object (i.e. translations and rotations only).
Special Affine transform
an affine transform where determinant of 3x3 part equals unity.
