There are two types of rotation transformation that we want to consider:
- Finite rotations, that is a change from one angular orientation to another.
- Continuous and infinitesimal rotations, such as when an object is continuously rotating.
When we first think of these types of rotation we might guess that one of these would be the rate of change of the other and that they would obey similar rules.
However it turns out that continuous and infinitesimal rotations are easily combined using vector addition. However finite rotations are more complicated and require other types of algebra.
Finite rotations
In 2 dimensions rotations can be combined by adding the angles. In 3 dimensions we need to multiply quaternions or matrices.
Can we extend this to more than 3 dimensions? This may not be very practical as our world only has 3 dimensions of space , however I'm hoping that this might give some insights into the nature of rotations.
Here are some approaches, that I can think of, for calculating the rotation of a given point in 3 dimensions:
- Calculate rotation around the axis of rotation.
- Translate the point to the rotation plane, rotate in the plane, then apply the reverse translation from the plane.
- Calculate the rotation as a sequence of two reflections.
In general a rotation occurs in a plane, that is a two dimensional space, which may be embedded in 3D space. It happens that in 3D planes and lines are duals and therefore one can be represented by the other, but this only applies in 3D space, therefore the first of the above methods only applies to 3D.
I will try to investigate whether the second two methods could apply to more than 3 dimensions (if more than 3 dimensions existed).
| Rotations in 'n' dimensions | |
| Rotations as 2 reflections |
Quadratic Form
Assuming that we are working in 'flat' (Euclidean) space then translations are linear, that is if a given translation moves a point a certain distance, then applying that translation twice will move the point twice that distance away.
However the effect of a rotation on a given point is not linear, in fact, the rotation has a quadratic form. For instance, if a given rotation rotates a point through 180 about the origin, then applying it twice will take it back to its original location, definitely not linear.
So why quadratic?
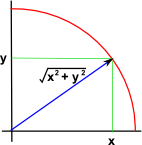
As we can see in this diagram, the length of the vector (shown in blue) depends on the square of the cartesian coordinates of its endpoint, when this vector os rotated around the origin this length remains the same.
Think about how to get from, a way to describe rotation which is intuitive, such as a set of angles and to turn that into a way to map the coordinates of an object before rotation to its coordinates after rotation. There are a number of mathematical notations and algebras that we could use, some are nearer to an angle like measure of rotation and some are nearer to the mapping of points. At some point in this sequence we need to do a quadratic transformation.
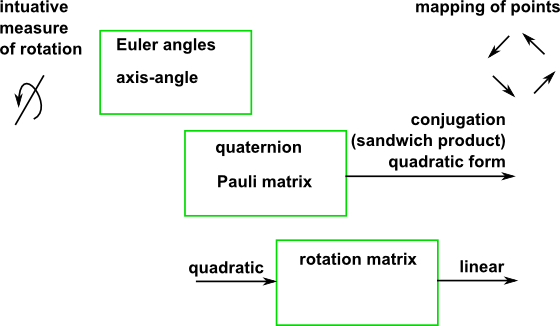
For instance, the quaternion or Pauli matrix cases are linear in terms of their inputs (a + i b + j c + k d) but the transform function is quadratic (Pout = q * Pin * conj(q)). However for a rotation matrix it is quadratic in terms of their inputs - something like this:
| [R] = |
|
but the transform function is linear.
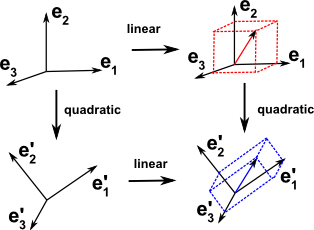
Another way of looking at this is that, a vector can be created from a linear combination of basis vectors, but to go from one set of basis vectors to another we need to use a quadratic form:
Spherical Geometry and 3D Rotation
There is a 1:1 equivalence (a morphism) between the rotation of a 3D rigid body and the movement of a shape on the surface of a sphere. Note that this is a shape rather than a point because we need to be able to specify a rotation θ in the spherical plane in addition to Latitude and Longitude. This gives us three degrees of freedom as with solid body rotation.
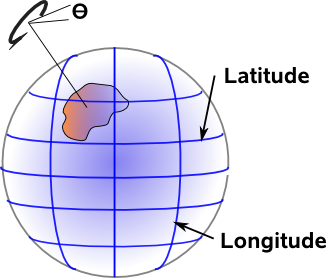
Perhaps a better way to look at this is to let the solid body be the sphere itself, then the surface of the sphere is automatically the same as rotation in 3D space. This equivalence seems almost trivial but if we can map the surface of the sphere to euclidean space then we can derive a model for isometries.
This equivalence described above is like mapping 3D rotations to the axis-angle representation.
What would be more useful would be to map rotations in 3D space to points in 4D space. To do this we need to map the rotations to points on a hypersphere, that is what quaternions do. By normalising quaternions to a unit hypersphere we are really mapping a 4D euclidean space to a curved 3D space.
This is discussed on the projective and conformal space pages.
Further Reading
This can be used to generate the matrix representation of the axis angle representation of rotation:

