Here we are concerned with properties of space, in addition to the number of dimensions, things like how 'flat' the space is and how the dimensions interact.
As we said here we can take the traditional geometry approach that many of us were taught at school; which involves two dimensional constructions with points, lines between points, angles between lines and trigonometry alternitivly we can use vectors which allow us to treat geometry problems in a more analytical way, allowing us to translate to an algebraic approach. However the disadvantage with vectors is that we need to choose a coordinate system which can be quite arbitrary and the results that we are looking for can get hidden by arrays of numbers which depend on the coordinate system that we chose.
There are ways to make our results independent of the coordinate system by expressing results in terms of general basis vectors by using tensor or geometric algebra.
In addition to the world we move in (two, three or more dimensional space) we may also be concerned with the dimension(s) of time (see pages about relativity). Time and space dimensions interact differently to dimensions of the same type and we reflect this in these models by whether the dimensions square to +ve or -ve.
Conventional 'flat' space, in which all the usual rules of geometry and trigonometry apply, is known as Euclidian space. When we get on to more advanced physics like special relativity we start to require other spaces like Minkowski space. We also use other types of space to make calculations easier, for instance, we may swap to a higher dimensional space to make the calculation of 3D rotations easier.
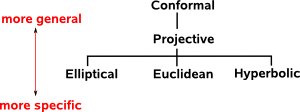
Ways to Catergorise Different Geometries
Euclids Postulates
| Euclidean | Spherical/Elliptical | Hyperbolic | Affine | ||
|---|---|---|---|---|---|
| postulate 1 | yes | yes | yes | yes | |
| postulate 2 | yes | no | yes | yes | |
| postulate 3 | yes | yes | yes | no | |
| postulate 4 | yes | yes | yes | no | |
| postulate 5 | yes | no | no | yes |
Kleins Erlangen Program
| Euclidean | Spherical/Elliptical | Hyperbolic | Affine | ||
|---|---|---|---|---|---|
| symmetry group | affinities |
Coordinates and metric
| space | coordinates | metric |
|---|---|---|
| Euclidian Space | Cartesian Coordinates | ||p - q||² = (p-q)•(p-q) |
| Affine Space | ||
| Projective Space | Homogeneous Coordinates | |
| Conformal Space | ||
| Minkowski Space | ||
| Barycentric Coordinates |
Coordinate Systems and Grids
Since Euclidean Space has no preferred origin or direction we need to add a coordinate system before we can assign numerical values to points and object in the space.
This coordinate system defines:
- The origin point.
- Directions as defined by a number of coordinates (which may or may not be orthogonal)
- Left or right coordinate system.
Modeling Points and Solid Objects
What is the simplest way to model the movement of things in these spaces?
The simplest case I can think of is the movement of solid objects in 2D euclidean space (or equivalently representing positions in 2D coordinate systems with different origins and orientations).
The simplest way that I can think of to do this is to use complex numbers with addition representing translation and multiplication (by cos(theta)+ i sin(theta)) representing rotation.
This has all the properties that we need to model this situation, if we multiply x + i y by its conjugate we get x² + y² and normal 'circular' trigonometry seems to apply.
So an algebra with one dimension that squares to +ve and the other squares to -ve seems to be the best way to model a space where both dimensions square to +ve.
So what happens if we use an algebra with two dimensions which square to +ve? The equivalent would be double numbers (also known as split-complex numbers) explained on this page. This is the same as complex numbers except instead of i²= -1 we have D²= +1. if we multiply x + D y by its conjugate we get x² - y² and 'hyperbolic' trigonometry seems to apply. This algebra is commutative, associative and distributive , division exists provided x ≠y and x ≠-y and there is no solution to square root of -ve numbers.
This seems to have all the characteristics to model one dimension of space and one dimension of time.
So the situation is the reverse of what might be expected:
- A space with signature '++' is modeled by an algebra with '+-'.
- A space with signature '+-' is modeled by an algebra with '++'.
Of course there are a lot of other factors, there are many ways to map the physical world to a type of algebra, but given the above model can we learn any lessons from this that we can use in higher numbers of dimensions? Would it work in higher dimensions if we reverse '+' -> '-' the non-real dimensions?
Rigid Transforms
There are alternative ways to represent how objects move in space, sometimes it would be better to combine translation and rotation into one operation rather than use addition for translation and multiplication. See pages about screw theory. There does not seem to be a 3D space which allows us to implement this directly, there seems to be a need to embed this into a higher dimensional space like Projective Space or Conformal Space.

