Equations
heading = atan2(2*qy*qw-2*qx*qz , 1 - 2*qy2 - 2*qz2)
attitude = asin(2*qx*qy + 2*qz*qw)
bank = atan2(2*qx*qw-2*qy*qz , 1 - 2*qx2 - 2*qz2)
except when qx*qy + qz*qw = 0.5 (north pole)
which gives:
heading = 2 * atan2(x,w)
bank = 0
and when qx*qy + qz*qw = -0.5 (south pole)
which gives:
heading = -2 * atan2(x,w)
bank = 0
Issues
The trig functions are many to one, therefore the inverse trig functions have
many possible results. We usually assume that:
acos returns the angle between 0 and π radians (equivalent to 0 and 180 degrees)
asin returns the angle between -π/2 and π/2 radians (equivalent to -90 and 90 degrees)
atan returns the angle between -π/2 and π/2 radians (equivalent to -90 and 90 degrees)
atan2 returns the angle between -π and π radians (equivalent to -180 and 180 degrees)
This is what the java Math functions return for instance. I think this makes
sense in the context of finding euler angles because we would usually want to
rotate the shortest angle to rotate.
If you have a different result from that shown on this page it may be that
you are using different standards, I have tried to keep the standards consistent
across this site and I have tried to define the standards that I am using here.
One of these standards is that the order that the euler rotations are applied
is 'NASA standard aeroplane' it uses a slightly different coordinate definition
from VRML (z and y axis swapped). Also when working with aeroplanes we often
work in terms of the position of external objects relative to the aircraft (i.e.
the inverse of its position transform as explained
here). therefore to get the expression normally used with NASA aeroplane
we invert all inputs (change sign of every term with odd number of sine terms)
invert output (conjugate quaternion) swap z and y for inputs (swap z and y columns)
swap z and y for outputs (swap z and y rows). In the case of aircraft it can
make sense to work in terms of the local frame of reference of the aircraft
looking out, I have a version of this page that does that here,
but be careful as this will no longer be compatible with the rest of this site.
However if you have checked these things and you still have a discrepancy then
I have probably made an error so please let me know here.
If you are working with different Euler Angles see the 'Alternative Euler Angle Sequences' section below.
Code
Java code to do conversion:
This depends on what conventions are used for the
Euler
Angles. The following assumes the standards
here
/** assumes q1 is a normalised quaternion */
public void set(Quat4d q1) {
double test = q1.x*q1.y + q1.z*q1.w;
if (test > 0.499) { // singularity at north pole
heading = 2 * atan2(q1.x,q1.w);
attitude = Math.PI/2;
bank = 0;
return;
}
if (test < -0.499) { // singularity at south pole
heading = -2 * atan2(q1.x,q1.w);
attitude = - Math.PI/2;
bank = 0;
return;
}
double sqx = q1.x*q1.x;
double sqy = q1.y*q1.y;
double sqz = q1.z*q1.z;
heading = atan2(2*q1.y*q1.w-2*q1.x*q1.z , 1 - 2*sqy - 2*sqz);
attitude = asin(2*test);
bank = atan2(2*q1.x*q1.w-2*q1.y*q1.z , 1 - 2*sqx - 2*sqz)
}
Note1: I have replaced Math.atan(a/b) with Math.atan2(a,b) as suggested by
Mark Elson
Note2: The cutoff point for singulaties is set to 0.499 and -0.499 which corresponds
to 86.3 degrees, this can be set closer to 90 if required but we have to accept
some inaccuracy around the singulaties. (Thanks to Jack Morrison
for corrections)
Note3: as suggested by minorlogic and Andy the above
expressions can be made to work with non-normalised quaternion (this saves a
CPU heavy square root operation). This uses 1=sqx + sqy + sqz + sqw so:
/** q1 can be non-normalised quaternion */
public void set(Quat4d q1) {
double sqw = q1.w*q1.w;
double sqx = q1.x*q1.x;
double sqy = q1.y*q1.y;
double sqz = q1.z*q1.z;
double unit = sqx + sqy + sqz + sqw; // if normalised is one, otherwise is correction factor
double test = q1.x*q1.y + q1.z*q1.w;
if (test > 0.499*unit) { // singularity at north pole
heading = 2 * atan2(q1.x,q1.w);
attitude = Math.PI/2;
bank = 0;
return;
}
if (test < -0.499*unit) { // singularity at south pole
heading = -2 * atan2(q1.x,q1.w);
attitude = -Math.PI/2;
bank = 0;
return;
}
heading = atan2(2*q1.y*q1.w-2*q1.x*q1.z , sqx - sqy - sqz + sqw);
attitude = asin(2*test/unit);
bank = atan2(2*q1.x*q1.w-2*q1.y*q1.z , -sqx + sqy - sqz + sqw)
}
Derivation of Equations
We can derive this by combining the formula derived in the matrix to euler page and the quaternion to matrix page, let me know if there is a more direct method, so starting with the matrix to euler page:
heading = atan2(-m20,m00)
attitude = asin(m10)
bank = atan2(-m12,m11)
We can combine this with the quaternion to matrix page:
| 1 - 2*qy2 - 2*qz2 |
2*qx*qy - 2*qz*qw |
2*qx*qz + 2*qy*qw |
| 2*qx*qy + 2*qz*qw |
1 - 2*qx2 - 2*qz2 |
2*qy*qz - 2*qx*qw |
| 2*qx*qz - 2*qy*qw |
2*qy*qz + 2*qx*qw |
1 - 2*qx2 - 2*qy2 |
So substituting this in above equation gives:
heading = atan2(2*qy*qw-2*qx*qz , 1 - 2*qy2 - 2*qz2)
attitude = asin(2*qx*qy + 2*qz*qw)
bank = atan2(2*qx*qw-2*qy*qz , 1 - 2*qx2 - 2*qz2)
This works at all points except the singularities at attitude = +90 and -90
degrees, at these points we will get atan2(0,0) for heading and bank which will
return 0 although this is not a valid result. We therefore need another way
to work out heading and bank at the singularities.
Singularities
Here we calculate how to detect the singularities and then how to represent them in terms of quaternions. the north pole is shown on the left and the south pole is shown on the right.
| Singularity at attitude = +90 degrees = straight up = north pole |
Singularity at attitude = -90 degrees = straight down = south pole |
this happens at attitude = +90 degrees:
attitude = asin(2*qx*qy + 2*qz*qw) = +90degrees
2*qx*qy + 2*qz*qw = 1
qx*qy + qz*qw = 0.5 |
this happens at attitude = -90 degrees:
attitude = asin(2*qx*qy + 2*qz*qw) = -90degrees
2*qx*qy + 2*qz*qw = -1
qx*qy + qz*qw = -0.5 |
from euler to quaternion page we have the result:
w = c1 c2 c3 - s1 s2 s3
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3
where:
- c1 = cos(heading / 2)
- c2 = cos(attitude / 2) if attitude = 90° then c2 = cos(45°) = 0.7071 if attitude = -90° then c2 = cos(-45°) = 0.7071
- c3 = cos(bank / 2)
- s1 = sin(heading / 2)
- s2 = sin(attitude / 2) if attitude = 90° then s2 = cos(45°) = 0.7071 if attitude = -90° then s2 = sin(-45°) = -0.7071
- s3 = sin(bank / 2)
|
So at attitude = +90°:
c2 = s2 = 0.7071
which gives:
w = 0.7071(c1 c3 - s1 s3)
x = 0.7071(s1 c3 +c1 s3)
y = 0.7071(s1 c3 + c1 s3)
z = 0.7071(c1 c3 - s1 s3)
apply trig addition formula:
sin(A+B) = sin A cos B + cos A sin B
cos(A+B) = cos A cos B - sin A sin B
which gives:
w = z = 0.7071(c(1+3))
x = y = 0.7071(s(1+3))
where:
- c(1+3) = cos((heading + bank)/2)
- s(1+3) = sin((heading + bank)/2)
therefore:
w = z = 0.7071(cos((heading + bank)/2))
x = y = 0.7071(sin((heading + bank)/2))
however asin and acos only give a 180 degree range and we want 360 degree range,
so divide one by other:
x/w = y/z = tan((heading + bank)/2)
so:
heading + bank = 2 * atan2(x,w)
in other words, when the aeroplane is flying straight up, it can be rotated
by both heading and bank and the rotation is the sum of both. In this case I
will choose to use heading and set bank to zero, so,
heading = 2 * atan2(x,w)
bank = 0 |
as before with north pole from euler
to quaternion page using attitude = -90°:
c2 = -s2 = 0.7071
which gives:
w = 0.7071(c1 c3 + s1 s3)
x = 0.7071(-s1 c3 +c1 s3)
y = 0.7071(s1 c3 - c1 s3)
z = 0.7071(-c1 c3 - s1 s3)
apply trig addition formula:
sin(A-B) = sin A cos B - cos A sin B
cos(A-B) = cos A cos B + sin A sin B
which gives:
w = -z = 0.7071(c(1-3))
-x = y = 0.7071(s(1-3))
where:
- c(1-3) = cos((heading-bank)/2)
- s(1-3) = sin((heading-bank)/2)
therefore:
w = -z = 0.7071(cos((heading-bank)/2))
-x = y = 0.7071(sin((heading-bank)/2))
however asin and acos only give a 180 degree range and we want 360 degree range,
so divide one by other:
x/w = y/z = -tan((heading-bank)/2)
so because -tan(x)=tan(-x) we get:
heading-bank = - 2 * atan2(x,w)
in other words, when the aeroplane is flying straight down, it can be rotated
by both heading and bank and the rotation is the difference of them. In this
case I will choose to use heading and set bank to zero, so,
heading = -2 * atan2(x,w)
bank = 0
Thanks to Vitor
Barata for correcting a previous error here. |
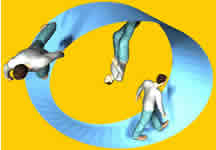
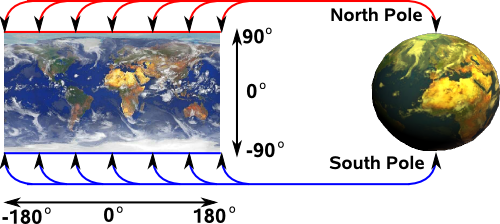
In order to try to get an intuative understanding of the singularities involved in converting other representations of 3D rotations to Euler angles it may help to look at the way we project the surface of a sphere onto a 2 dimensional map. This is a different case and it only involves two angles, latitude and longitude, but this simpler example may show the principles. This analogy is explained in more detail on this page.
At the north
and south poles longitude does not matter so
if we are converting some other description of north pole to latitude, longitude
it might give any value for longitude, for example, infinity. So we have to
be very careful at these points.
Similarly we can map Euler angles to quaternions (4 dimensional hypersphere). This maps a one dimensional space (rotations around 0,1,0 axis) to a two dimensional plane in Euler terms. This is where attitude = 90° and heading, bank vary:
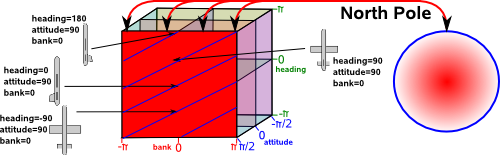
On this plane lines of common orientation are diagonal lines, that is rotation around 0,1,0 axis are given by angle = heading+bank.
Similarly for the south pole.
Example
| we take the 90 degree rotation from this: |
 |
to this: |
 |
As shown
here the quaternion for this rotation is: (0.7071+ i 0.7071)
So using the above result:
sqw = q1.w*q1.w = 0.5
sqx = q1.x*q1.x = 0.5
sqy = q1.y*q1.y = 0
sqz = q1.z*q1.z =0
heading = atan2(2.0 * (q1.x*q1.y + q1.z*q1.w),(sqx - sqy - sqz + sqw)) = atan2(0,2)
= 0
bank = atan2(2.0 * (q1.y*q1.z + q1.x*q1.w),(-sqx - sqy + sqz + sqw)) = atan2(0.5,0)
= 90 degrees
attitude = asin(-2.0 * (q1.x*q1.z - q1.y*q1.w)/sqx + sqy + sqz + sqw) = asin(0/2)
= 0
So this gives the correct result shown here,
it is banking by 90 degrees, but we have to be very careful about the following
issues:
- If we had not used the atan2 function then one of the intermediate steps
would involve infinity (division by 0) therefore most maths libraries have
an atan2 function to avoid this step.
- Most maths libraries use radians instead
of degrees (apart from OpenGL).
Alternative Euler Angle Sequences
I am trying to make this site consistant and therefore I have standarised on one Euler angle sequence as defined on this page. However there are often reasons to use different Euler angle sequences:
- You may be working with a program which uses a different Euler angle sequence.
- You may need the singularities to be at different angles so they are less likely to cause problems.
- The objects that you are modelling may just favor a different set of angles.
Amy de Buitléir has written this document and kindly allowed me to publish it here. This shows how to convert a quaternion to any Euler angle sequence. Instead of defining the quaternion in terms of rotations about the absolute coordinates i, j and k the document defines 3 mutually perpendicular axes e1, e2 and e3. So, to generate the mapping for a given set of Euler angles the user needs to map e1, e2 and e3 to i, j or k in the appropriate order. This involves the value e which seems to define a sort of left or right handedness, but on its own this is not enough to define the Euler angle sequence, will still need to define the e1, e2, e3 to i, j, k mapping.
Angle Calculator and Further examples
I have put a java applet here which allows the values to be entered and the converted values shown along with a graphical representation of the orientation.
Also further examples in 90 degree steps here
Or enter the quaternion below, then click calculate to get the heading, attitude and bank in degrees.
This site may have errors. Don't use for critical systems.