Overview
Here we are looking at the collision of 2D rigid objects. Although we live in a 3 dimensional world we can think of this 2D example as a special case where the objects are constrained so that their velocities can be represented in a plane.
We can't use identical equations to the 3D case because the vector cross product does not apply to 2D vectors. We will therefore start analysing this in terms of individual scalar components, this may make the equations quite long but there are less mathematical concepts to learn.
Modeling collisions involves a lot of assumptions and approximations, also the concept of an 'impulse' is not always intuitively obvious. These issues are all discussed on the page above this and it may be worth reading that page before this.
One difficult bit is understanding how to work with objects that have both rotation and linear motion. The main method we will use to do this involves the following stages.
- Determine the collision point and the normal direction at this point.
- Calculate the minimum impulse to prevent the objects intersecting, or to
reverse the approach velocity, depending on the coefficient of friction.
- Calculate the effect of this impulse on the rotation and linear motion
separately.
If you would like to see a practical example of this see this page (sent to me by Kevin Pegrume) which demonstrates this and highlights some of the counter intuitive issues.
Results
Here are equations for calculating the two components of impulse (J) in the x and y dimensions. Then the equations to use this to calculate the new velocities.
This is just an overview, we will define the terms and give the derivation later:
| |
General case |
| impulse
= |
Jx = (e+1)/k * (Vaix - Vbix)( 1/ma - rax2/Ia + 1/mb - rbx2/Ib)
- (e+1)/k * (Vaiy - Vbiy) (rax ray / Ia + rbx rby / Ib)
Jy = - (e+1)/k * (Vaix - Vbix) (rax ray / Ia + rbx rby / Ib) + (e+1)/k
* (Vaiy - Vbiy) ( 1/ma - ray2/Ia + 1/mb - rby2/Ib)
where:
k=1/ma2+ 2/(ma*mb) +1/mb2 - rax2/(ma*Ia)
- rbx2/(ma*Ib) - ray2/(ma*Ia) - ray2/(mb*Ia) -
rax2/(mb*Ia) - rbx2/(mb*Ib) - rby2/(ma*Ib) - rby2/(mb*Ib)
+ ray2 rbx2/(Ia*Ib) + rax2 rby2/(Ia*Ib)
- 2 rax ray rbx rby/(Ia*Ib)
|
Final velocity of object a=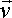 af
= af
= |
Vaix - Jx/Ma
Vaiy - Jy/Ma |
Final velocity of object b=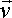 bf
= bf
= |
Vbix - Jx/Mb
Vbiy - Jy/Mb |
| Final angular velocity of object a=waf
= |
waix - (Jx ray - Jy rax) /Ia
waiy - (Jx ray - Jy rax) /Ia
|
| Final angular velocity of object b=wbf
= |
wbix - (Jx rby - Jy rbx) /Ib
wbiy - (Jx rby - Jy rbx) /Ib |
Derivation
As with the 1D case we can start with the definition of the coefficient of
restitution which is the ratio of converging and diverging velocities.
However, in this case, the velocities are not the velocities of the centre
of mass, they are the velocities of points (in absolute coordinates) on the
solid bodies, these are the points on the bodies that actually collide.
e = (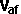 -
- 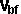 )
/ (
)
/ (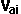 -
- 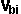 )
)
| where: | |
symbol |
description |
type |
units |
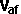 |
final velocity of collision
point on object a |
vector |
m/s |
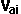 |
initial velocity of collision
point on object a |
vector |
m/s |
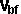 |
final velocity of collision
point on object b |
vector |
m/s |
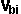 |
initial velocity of collision
point on object b |
vector |
m/s |
| e |
coefficient of restitution which depends on the nature of the two colliding
materials |
scalar |
none |
let ΔVa
= 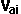 -
- 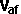
This is the change in velocity of the collision point on body 'a' due to the
impulse.
and ΔVb
= 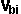 -
- 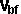
This is the change in velocity of the collision point on body 'b' due to the
impulse.
so,
e * (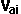 -
- 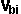 )=
-(
)=
-(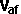 -
- 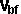 )
)
(e+1) * (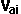 -
- 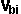 )=
-(
)=
-(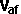 -
- 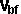 )+(
)+(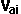 -
- 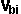 )
)
(e+1) * (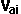 -
- 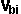 )=
ΔVa + ΔVb
)=
ΔVa + ΔVb
We can split this vector into two seperate scalar equations:
(e+1) * (Vaix - Vbix)= ΔVax
+ ΔVbx
(e+1) * (Vaiy - Vbiy)= ΔVay
+ ΔVby
The way that ΔVa
and ΔVb are
related to impulse (J) is explained on this
page, from that page we get:
ΔVpx = Jx
( 1/m - ry2/I) + Jy rx ry / I
ΔVpy = Jx
rx ry / I + Jy ( 1/m - rx2/I)
| where: | |
symbol |
description |
type |
units |
| Vp = linear velocity of a particle on a solid body |
Vp = linear velocity of a particle on a solid body |
|
|
| J |
impulse |
|
|
| I |
inertia scalar such that torque = I * alpha (only true when object is
symmetrical) |
scalar |
|
| [I] |
inertia tensor |
3x3 matrix |
|
| m |
mass |
scalar |
kg |
| r |
position of particle relative to centre of mass (vector) - Note: this
is in absolute coordinates, not local body coordinates, so this will be a
function of time as the body rotates. |
vector |
m |
So we get:
(e+1) * (Vaix - Vbix)= Jx ( 1/ma - ray2/Ia) + Jy rax ray / Ia +
Jx ( 1/mb - rby2/Ib) + Jy rbx rby / Ib
(e+1) * (Vaiy - Vbiy)= Jx rax ray / Ia + Jy ( 1/ma - rax2/Ia) + Jx
rbx rby / Ib + Jy ( 1/mb - rbx2/Ib)
We want to solve this for J, to do this we need to separate out the J terms
on the right hand side.
(e+1) * (Vaix - Vbix)= Jx ( 1/ma - ray2/Ia + 1/mb - rby2/Ib)
+ Jy (rax ray / Ia + rbx rby / Ib)
(e+1) * (Vaiy - Vbiy)= Jx (rax ray / Ia + rbx rby / Ib) + Jy ( 1/ma - rax2/Ia
+ 1/mb - rbx2/Ib)
inverting gives:
Jx = (e+1)/k * (Vaix - Vbix)( 1/ma - rax2/Ia + 1/mb - rbx2/Ib)
- (e+1)/k * (Vaiy - Vbiy) (rax ray / Ia + rbx rby / Ib)
Jy = - (e+1)/k * (Vaix - Vbix) (rax ray / Ia + rbx rby / Ib) + (e+1)/k * (Vaiy
- Vbiy) ( 1/ma - ray2/Ia + 1/mb - rby2/Ib)
where:
k=1/ma2+ 2/ma mb +1/mb2 - rax2/maIa - rbx2/maIb
- ray2/maIa - ray2/mbIa - rax2/mbIa - rbx2/mbIb
- rby2/maIb - rby2/mbIb + ray2 rbx2/IaIb
+ rax2 rby2/IaIb - 2 rax ray rbx rby/IaIb
Code
/**
This function calulates the velocities after a 2D collision vaf, vbf, waf and wbf from information about the colliding bodies
@param double e coefficient of restitution which depends on the nature of the two colliding materials
@param double ma total mass of body a
@param double mb total mass of body b
@param double Ia inertia for body a.
@param double Ib inertia for body b.
@param vector ra position of collision point relative to centre of mass of body a in absolute coordinates (if this is
known in local body coordinates it must be converted before this is called).
@param vector rb position of collision point relative to centre of mass of body b in absolute coordinates (if this is
known in local body coordinates it must be converted before this is called).
@param vector n normal to collision point, the line along which the impulse acts.
@param vector vai initial velocity of centre of mass on object a
@param vector vbi initial velocity of centre of mass on object b
@param vector wai initial angular velocity of object a
@param vector wbi initial angular velocity of object b
@param vector vaf final velocity of centre of mass on object a
@param vector vbf final velocity of centre of mass on object a
@param vector waf final angular velocity of object a
@param vector wbf final angular velocity of object b
*/
CollisionResponce(double e,double ma,double mb,matrix Ia,matrix Ib,vector ra,vector rb,vector n,
vector vai, vector vbi, vector wai, vector wbi, vector vaf, vector vbf, vector waf, vector wbf) {
double k=1/(ma*ma)+ 2/(ma*mb) +1/(mb*mb) - ra.x*ra.x/(ma*Ia) - rb.x*rb.x/(ma*Ib) - ra.y*ra.y/(ma*Ia)
- ra.y*ra.y/(mb*Ia) - ra.x*ra.x/(mb*Ia) - rb.x*rb.x/(mb*Ib) - rb.y*rb.y/(ma*Ib)
- rb.y*rb.y/(mb*Ib) + ra.y*ra.y*rb.x*rb.x/(Ia*Ib) + ra.x*ra.x*rb.y*rb.y/(Ia*Ib) - 2*ra.x*ra.y*rb.x*rb.y/(Ia*Ib);
double Jx = (e+1)/k * (Vai.x - Vbi.x)( 1/ma - ra.x*ra.x/Ia + 1/mb - rb.x*rb.x/Ib)
- (e+1)/k * (Vai.y - Vbi.y) (ra.x*ra.y / Ia + rb.x*rb.y / Ib);
double Jy = - (e+1)/k * (Vai.x - Vbi.x) (ra.x*ra.y / Ia + rb.x*rb.y / Ib)
+ (e+1)/k * (Vai.y - Vbi.y) ( 1/ma - ra.y*ra.y/Ia + 1/mb - rb.y*rb.y/Ib);
Vaf.x = Vai.x - Jx/Ma;
Vaf.y = Vai.y - Jy/Ma;
Vbf.x = Vbi.x - Jx/Mb;
Vbf.y = Vbi.y - Jy/Mb;
waf.x = wai.x - (Jx*ra.y - Jy*ra.x) /Ia;
waf.y = wai.y - (Jx*ra.y - Jy*ra.x) /Ia;
wbf.x = wbi.x - (Jx*rb.y - Jy*rb.x) /Ib;
wbf.y = wbi.y - (Jx*rb.y - Jy*rb.x) /Ib;
}
Other Methods
Collision in 2 dimensions (head-on collision, no rotation,
no friction)
This is the simplest case where the direction of travel of both objects and
the impact point are all along the same line:
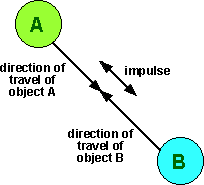
In this case the results are similar to the one
dimensional case except that the velocities are expressed as two dimensional
vectors.
For the definitions and working of this case
see here.
Collision in 2 dimensions (no rotation, no friction)
In the perfectly elastic case there are 4 unknowns (2 dimensions of velocity
of object a + 2 dimensions of velocity of object b) and the conservation laws
only give us 3 equations (conservation of momentum in 2 dimensions + conservation
of scalar energy). Therefore the conservation laws are not enough to solve this.
In the perfectly inelastic case the two objects will have the same final velocity
in the direction of the impulse only.
The result will depend on the geometry, for example in the following example
the impulse is not along the direction of travel:
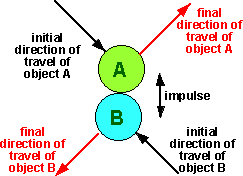
Whereas, in the following case the impulse is along the direction of travel:
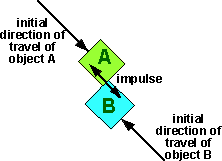
So the first thing is to decide the direction of the impulse 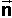 ,
if there is no friction then the impulse will be normal to the surface at the
collision point. Once we know
,
if there is no friction then the impulse will be normal to the surface at the
collision point. Once we know 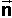 then
we can work out the magnitude of the impulse.
then
we can work out the magnitude of the impulse.
For the perfectly elastic case the impulse will be:
2*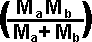 * ((
* ((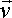 ai
-
ai
- 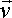 bi)•
bi)•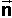 ) *
) * 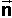
For the perfectly inelastic case the impulse will be:
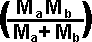 * ((
* ((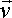 ai
-
ai
- 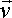 bi)•
bi)•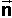 )
*
)
* 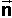
Due to the dot product operation the result of (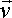 ai
-
ai
- 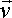 bi)•
bi)•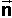 is a scalar, but we want this to act in the direction of the impulse so we multiply
by
is a scalar, but we want this to act in the direction of the impulse so we multiply
by 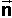 to give a vector.
to give a vector.
| where: | |
symbol |
description |
type |
units |
| Ma |
mass of object a |
scalar |
kg |
| Mb |
mass of object b |
scalar |
kg |
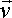 ai ai |
initial velocity of object a |
vector |
m/s |
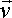 bi bi |
initial velocity of object b |
vector |
m/s |
| • |
dot product operation (see
vectors here) |
|
|
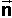 |
unit vector in the direction
of the impulse |
vector |
|
This case is not very practical. It would be quite difficult to arrange a collision
where the objects are free to move in 2 dimensions but are prevented from rotation,
however it is a step toward the more general case.
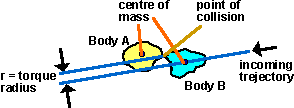
Collision in 2 dimensions (with rotation no friction)
In this case we include the posibility that rotation may be transferred or
generated by the collision.
In the following example the approach velocity and the normal are in the same
direction, also the objects have no initial angular velocity, rotation will
be generated because the line from the centre of mass to the collision point
is not in the same direction.
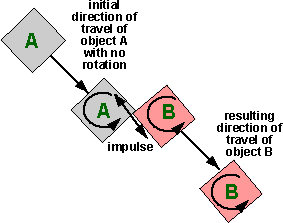
Collision in 2 dimensions (with rotation and friction)
In the following example the objects hit head-on, however due to the rotation
and friction, the impulse is at a different angle to the approach velocity and
to surface normal. This impulse tends to reduce the angular speed of A and to
cause B to rotate in the opposite direction.
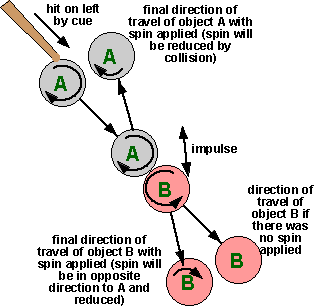
For more about this example
see here.
For further information see:
The conservation of energy and conservation of momentum laws above are not
enough to calculate the final rotations or directions. These will depend on
the geometry of the object and where on the objects they hit, if it hits on
on side it may go spinning off in one direction, if it hits on the other side
it will go off spinning in a different direction.
In this case the bodies can rotate around their centre-of-mass. The rotations
after the collision will be different than before the collision depending on
the angles between the centres of mass and the point of impact.
Let:
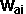 is initial angular speed of body
a in radians per sec
is initial angular speed of body
a in radians per sec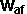 is final angular speed of body
a in radians per sec
is final angular speed of body
a in radians per sec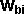 is initial angular speed of body
b in radians per sec
is initial angular speed of body
b in radians per sec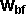 is final angular speed of body
b in radians per sec
is final angular speed of body
b in radians per sec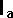 moment of inertia of body a about
its centre of mass.
moment of inertia of body a about
its centre of mass.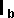 moment of inertia of body b about
its centre of mass.
moment of inertia of body b about
its centre of mass.
 conservation of energy:
conservation of energy:
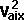 *
* 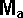 +
+ 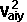 *
* 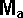 +
+ 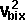 *
*  +
+ 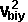 *
*  +
+ 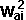 *
* 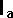 +
+ 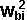 *
* 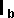
= 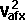 *
* 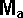 +
+ 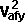 *
* 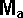 +
+  *
*  +
+ 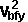 *
*  +
+ 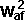 *
* 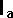 +
+ 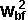 *
* 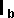
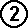 conservation of momentum in x
dimension:
conservation of momentum in x
dimension:
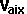 *
* 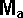 +
+ 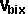 *
*  =
= 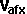 *
* 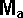 +
+ 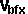 *
* 
 and conservation of momentum
in y dimension:
and conservation of momentum
in y dimension:
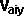 *
* 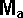 +
+ 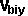 *
*  =
= 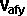 *
* 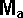 +
+ 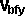 *
* 
Conservation of angular momentum about centre of mass of whole system (see
here for derivation)
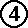
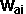 *
* 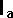 +
+ 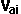 *
*
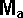 *dac +
*dac + 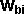 *
*
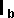 +
+ 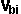 *
*
 * dbc=
* dbc= 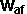 *
*
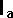 +
+ 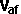 *
*
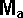 *dac +
*dac + 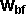 *
*
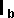 +
+ 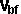 *
*
 * dbc
* dbc
so we have 4 equations an 6 unknowns (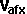 ,
, 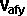 ,
, 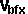 ,
,
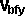 ,
, 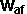 and
and 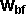 )
)
I think we need two more to be something about how energy is translated to
angular motion from linear motion or back. This depends on how the centres of
mass and collision point line up:
Imagine that all the linear motion is converted into angular motion by the
collision in a very short time (t)
Linear impulse F * t = m (v2 - v1)
converted into Angular impulse T * t = I (w2 - w1)
and T = F * r
so 't' cancels out and gives:  * (
* (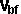 -
- 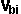 )
* rb =
)
* rb = 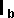 * (
* (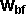 -
- 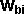 )
)
But only some of the energy will be converted between linear and angular momentum.
I guess that during the collision there will be a reaction at the point of collision
At this point I was stuck until I got the following message from Chris Rodrigues:
|
From: "C Rodrigues"
To: Martin Baker
Sent: Sunday, September 23, 2001 6:17 AM Subject: 3d Physics: Collision
modeling
Martin B,
I was working on the problem of modeling collisions in 2d when I found
your page. It gave me an idea on how to proceed. I started from the fact
that, for rigid bodies in an inelastic collision with no friction, the
velocity of each body at the point of collision will be the same, i.e.
the two bodies will stick together. (Wish I could draw you a picture.)
More precisely, the component of velocity normal to the surface at the
point of collision will be the same. This produces a single equation to
solve. The unknown variable is the magnitude of the impulse required to
satisfy the condition. Without friction, the impulse will be normal to
the surface of collision.
Here is the algebra how I would solve the collision without friction
problem for two dimensions:
For vectors * represents dot product, x represents scalar cross product
(v1.x * v2.y - v2.x * v1.y).
I also write +90deg to mean rotate a vector 90 degrees counterclockwise.
Given object a with position Ra (vector), initial velocity Va, mass Ma,
initial angular velocity Wa, moment Ia, object b with analogous characteristics,
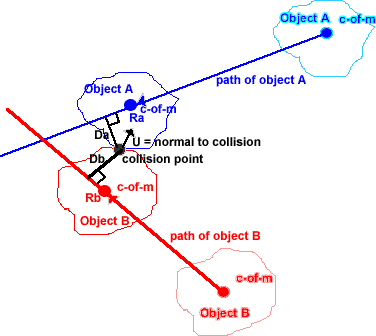
point of collision Rc, unit vector perpendicular to the surface of collision,
pointing into object a called U,magnitude of impulse i:
final velocity of collision point on a = final velocity of collision
point on b
old velocity of collision point on a + change in velocity of collision
point on a = old velocity of collision point on b + change in velocity
of collision point on b
old velocity of collision point on a - old velocity of collision point
on b = change in velocity of collision point on b - change in velocity
of collision point on a
the right side of the equation, after some simplification, is
i * (1/Ma + 1/Mb + ((Rc - Ra) x U)^2/Ia + ((Rb - Ra) x U)^2/Ib)
Since i is the only unknown in the equation, it can be solved.
i = -(Va + Wa * (Rc - Ra)+90deg - Vb - Wb * (Rc - Rb)+90deg) * U / (
1 / Mb + 1/Ma + U * (Rc - Rb)+90deg)^2 + U * (Rc - Rb)+90deg)^2 )
This is the impulse on object a; the negative of i is the impulse on
object b. Now the new velocities of objects a and b can be calculated.
It's worth noting that elastic collisions are covered simply by multiplying
the impulse on both bodies by 2. Also, the method for solving can be extended
to three dimensions.
The simulation I made using this method works well for objects of different
masses, but it causes objects to spin too fast. I do not know whether
the problem is with the formula or with my programming.
Please e-mail me back with your thoughts, or if I didn't explain something
clearly.
-Chris
|
With help fromChris, Here is the method:
(the following diagram may not be ideal because, if the shapes have corners,
it is difficult to know what the normal vector U should be. However we do need
to be able to cope with this case.)
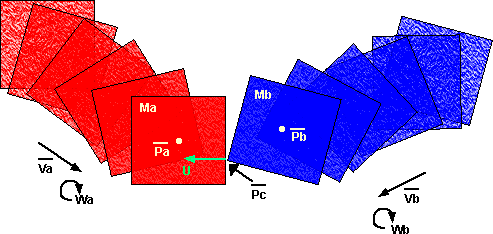
impulse on a = integral of force over time, (change in momentum of the colliding
objects)
In this case we are considering the impulse to consist of a component which
is changing the linier momentum and a component changing the angular momentum,
ie:
impulse on a = i = component of impulse changing linear motion + component
of impulse changing rotational motion
In the case of linier motion component, this is the change of linier momentum,
which is i = Δv * M
so for object a this is i=(Va - Vaf) Ma
where:
- Vaf is the final velocity
In the case of angular motion component:
net Torque = T = d L/ d t = F x R = F * ((Rc -r)+90deg * U)
where:
- T is net instantanous Torque (in this case caused only by instantanous contact
force)
- L is angular momentum
- x is cross product
- F is force acting on contact point
- R is distance between centre of mass and contact point
- r is centre of mass of object
- Rc is contact point
- U is unit vector normal to contact point
so change in angular momentum is:
d L = F dt * ((Rc -r)+90deg * U)
so impulse due to angular motion is:
i = intergral of F dt
i = d L / ((Rc -r)+90deg * U)
i = Δw* I / ((Rc -r)+90deg * U)
where:
so total impulse due to linear and angular momentum is:
i = Δv * M = Δw* I / ((Rc -r)+90deg * U)
Perfectly inelastic collision case
Final Velocities for perfectly inelastic collision case
conservation of momentum applies independantly of rotation, so,
va * Ma + vb * Mb = vf * (Ma + Mb)
where:
- va = initial velocity vector of object a
- Ma = mass of object a
- vb = initial velocity vector of object b
- Mb = mass of object b
- vf = final velocity vector of both objects
so
vf = 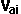 * * 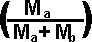 + +
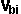 * * 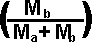
apply conservation of angular momentum
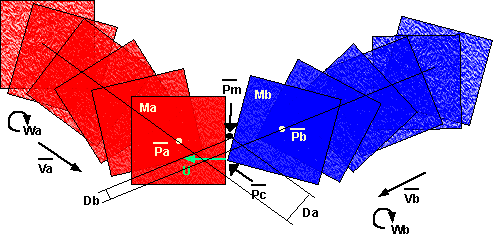
choose to measure all angular momentums around the common centre of mass
(Pm).
Because this is inelastic case I have assumed that, on collision, the
two objects stick together instantly, held on these relative positions
and rotating about their common centre of mass. I could not find a way
to allow them to be fixed normal to the direction of impact but allow
them to slide along the point of imact. (because both objects are rotating).
before the collision angular momentum is the sum of the angular momentums
due to spin + the sum of angular momentums due orbiting about Pm.
Ia * Wa + Da * Ma Va + Ib * Wb + Db * Mb Vb
after the collision the angular momentum about the same point is
Wf ( Ma * (Pa-Pm)^2 + Ia +Mb * (Pb-Pm)^2 + Ib)
By conservation of angular momentum these two are equal:
Ia * Wa + Da * Ma Va + Ib * Wb + Db * Mb Vb = Wf ( Ma * (Ra-Rm)^2 + Ia
+Mb * (Rb-Rm)^2 + Ib)
Wf = (Ia * Wa + Da * Ma Va + Ib * Wb + Db * Mb Vb) /( Ma * (Ra-Rm)^2
+ Ia +Mb * (Rb-Rm)^2 + Ib)
where:
Rm = common centre of mass = (Ra * Ma + Rb * Mb )/ (Ma + Mb)
Rb - Rm = (Rb Ma + Rb Mb - Ra * Ma - Rb * Mb)/ (Ma + Mb) = (Rb - Ra)
* Ma / (Ma + Mb)
Ra - Rm = (Ra Ma + Ra Mb - Ra * Ma - Rb * Mb)/ (Ma + Mb) = (Ra - Rb)
* Mb / (Ma + Mb)
so:
Wf = (Ia * Wa + Da * Ma Va + Ib * Wb + Db * Mb Vb) /( Ma * ((Ra - Rb)
* Mb / (Ma + Mb))^2 + Ia +Mb * ((Rb - Ra) * Ma / (Ma + Mb))^2 + Ib)
Wf = (Ia * Wa + Da * Ma Va + Ib * Wb + Db * Mb Vb) /( Ia + Ib + Ma *
((Ra - Rb) * Mb / (Ma + Mb))^2 +Mb * ((Rb - Ra) * Ma / (Ma + Mb))^2)
Wf = (Ia * Wa + Da * Ma Va + Ib * Wb + Db * Mb Vb) /( Ia + Ib + Ma *
((Ra - Rb)^2 * Mb^2 +Mb * ((Rb - Ra) ^2* Ma^2) / (Ma + Mb)^2)
Wf = (Ia * Wa + Da * Ma Va + Ib * Wb + Db * Mb Vb) /( Ia + Ib + (Ma +
Mb)*Ma*Mb (Ra - Rb)^2 / (Ma + Mb)^2)
calculate i on object a
The forces that change the motion of the objects must do three things
during the collision:
- Change the linier velocity of the centre of gravity of the two objects
- Change the angular rotations of the two objects about their own centres
of mass
- Make the two objects orbit around their common centre of mass
Item 3 is a continous force and not really an impulse. So take the impulse
as being items 1 & 2 only.
To simplify the equation
let-
ra = ((Rc -Ra)+90deg * U)
so:
i = (Va-Vf) * Ma + (Wa-Wf)* Ia / ra
= (va Mb - vb * Mb)/(Ma + Mb)) * Ma + ( (Ia * Wa + Da * Ma Va + Ib *
Wb + Db * Mb Vb) /( Ia + Ib + (Ma + Mb)*Ma*Mb (Ra - Rb)^2 / (Ma + Mb)^2))*
Ia / ra
= ((va - vb) * Mb*Ma)/(Ma + Mb)) + ( (Ia * Wa + Da * Ma Va + Ib * Wb
+ Db * Mb Vb) /( Ia + Ib + (Ma + Mb)*Ma*Mb (Ra - Rb)^2 / (Ma + Mb)^2))*
Ia / ra) )
|
This site may have errors. Don't use for critical systems.










