When we looked at vectors we saw that they must have two operations addition and scalar multiplication.
| operation | notation | explanation |
|---|---|---|
| addition | V(a+b) = V(a) + V(b) | the addition of two vectors is done by adding the corresponding elements of the two vectors. |
| scalar multiplication | V(s*a) = s * V(a) | a scalar product of a vector is done by multiplying the scalar product with each of its terms individually. |
These operations interact according to the distributivity property: s*(b+c)=s*b+s*c
In addition to these operations we can have other operations which we can apply to vectors such as the vector cross product:
Vector Cross Product
Unlike the scalar product, both the two operands and the result of the cross product are vectors.
The vector cross product has some useful properties, it produces a vector which is mutually perpendicular to the two vectors being multiplied.
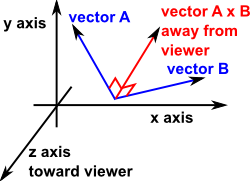
The resulting vector A × B is defined by:
x = Ay * Bz - By * Az
y = Az * Bx - Bz * Ax
z = Ax * By - Bx * Ay
where x,y and z are the components of A x B
The scalar length of A×B is,
|A × B| = |A| * |B| * sin(θ)
where θ is the angle between A and B.
The cross product interpretation only to 3D vectors. For instance in 2 dimensions it is not possible to find another vector which is mutually perpendicular to 2 arbitrary vectors, in 4 dimensions (or greater) there are many vectors which are mutually perpendicular to 2 arbitrary vectors.
The cross product can be used to calculate the Normal to a surface as shown here.
ExampleIn the above diagram it is is difficult to draw the directions to clearly represent all 3 dimensions. So I thought it would help check the direction by working out an example using approximate direction: If we let: Vector A be in the y direction (Ax=0 , Ay=1 , Az = 0) so, Vector A×B components: x = Ay * Bz - By * Az = 0 so, AxB = (0 , 0 , -1) = away from viewer |
The cross product is also given by the determinant:
| i | j | k |
| Ax | Ay | Az |
| Bx | By | Bz |
where: i,j & k are unit vectors in the x,y and z dimensions.
Important Issues
We must be careful, when doing vector algebra with cross multiplication, because we can't use the usual rules:
- Vector cross products only apply to vectors in 3 or 7 dimensions. (one dimension less than the division algebras quaternion=4,octonion=8).
- Vector cross products do not commute, they anticommute (A×B = -B×A) this is not nessesarity a bad thing, for instance 3D rotation does not commute, but we have to be careful.
- Vector cross products are not associative, they are anti-associative((A × B) × C may not equal A × (B × C))
- A vector squared is zero.
- Cross multiplication does not have a unique inverse.
- There is no identity element I × A = A
Identities
| A×B + B×A = 0 | anti-commutative, vector cross multiplication is not commutative, changing the order reverses the direction of the resulting vector: A×B = - B×A. |
| A×(B×C) + B ×(C×A) + C ×(A×B) = 0 |
Jacobi identity : anti-associative : anti-symmetry |
| A × A = 0 | A 'squared' is a zero length vector because sin(0) = 0 |
| A × (B + C) = (A × B) + (A × C) | cross multiplication for vectors is distributive over + |
| 0 × A = 0 |
Where:
- A,B and C = any vectors
- 0 = zero length vector (all elements are zero)
- × = vector cross product
For example, the following expression:
A × A × B
We might expect that this is zero, because A x A = 0, but this is not necessarily so because cross multiplication is not associative. We need to specify the order, if it is:
A × (A × B)
then the result is not necessarily zero.
Related Multiplications
There are generalisations to vector algebra, for example,
| Clifford Algebra | In particular the exterior product of Grassmann algebra which is incorporated into Clifford algebra. |
| Lie Algebra | Lie algebra is a linerasation of Lie groups and therefore relates this topic to groups and symmetries. |
The Grassmann exterior product has much nicer properties than the cross product:
- The Grassmann product applies in any number of dimensions.
- The Grassmann product is associative.
Comparison to Exterior Product
The exterior product combines two vectors and produces a bivector. In three dimensions the bivector has similar properties to a vector and so, for many purposes, can be treated as a vector. For instance the multiplication table for the cross product is:
a×b |
b.e1 | b.e2 | b.e3 |
| a.e1 | 0 | e3 | -e2 |
| a.e2 | -e3 | 0 | e1 |
| a.e3 | e2 | -e1 | 0 |
The exterior multiplication table is:
a/\b |
b.e1 | b.e2 | b.e3 |
| a.e1 | 0 | e1/\e2 | -e3/\e1 |
| a.e2 | -e1/\e2 | 0 | e2/\e3 |
| a.e3 | e3/\e1 | -e2/\e3 | 0 |
So the result of the two types of multiplication is virtually the same, the difference is that the exterior multiplication produces a bivector and not a vector. The important thing is that multiplication table of a vector /\ bivector is not the same as vector /\ vector, in fact the multiplication table of vector /\ bivector is like the dot product of vector • vector.
So when we have triple multiplications, they are associative, the exterior product of 3 vectors, A, B and C gives the volume enclosed by the three vectors:
A /\ B /\ C
This is equivalent to this equation of cross and dot products:
(A × B) • C
Duality between vectors and bivectors in 3 dimensions
This duality only applies to three dimensions, if two 2-dimentional vectors are cross multiplied the bivector is one dimensional, if two 4-dimentional vectors are cross multiplied the bivector is 6-dimentional. bivectors are discussed here.
In three dimensional vector algebra only, a bivector also has three dimensions, so for most purposes (in three dimensions) we can treat the result of a cross product as a vector.
Skew Symmetric Matrix
We can also work out a 3x3 skew symmetric matrix which is equivalent to the cross product, in other words, if,
C = A × B
Then we can find a skew symmetric matrix [~A] such that:
C = [~A] B
This matrix is:
| [~A] = |
|
As described here.
Code:
The following is Java code for vector cross product.
Void cross(sfvec3f other) {
double xh = y * other.z - other.y * z;
double yh = z * other.x - other.z * x;
double zh = x * other.y - other.x * y;
x = xh;
y = yh;
z = zh;
}
The following is managed C++ code for vector cross product.
Void sfvec3f::cross(sfvec3f* other) {
double xh = y * other->z - other->y * z;
double yh = z * other->x - other->z * x;
double zh = x * other->y - other->x * y;
x = xh;
y = yh;
z = zh;
}
This method will be used by the sfvec3f class.
Further Reading
Vectors can be manipulated by matrices, for example translated, rotated, scaled, reflected.
There are mathematical objects known a multivectors, these can be used to do many of the jobs that vectors do, but they don't have some of the limitations (for example vector cross product is limited to 3 dimensions and does not have an inverse).


