Maths - Transformations using Quaternions

On this page we are mostly concerned with using quaternions for working with rotations. Other transformations, such as scale transforms, are possible but tend to be less used in practice. So I will often use the more general word 'transform' even though the word 'rotation' could be used in many cases.

There are two types of algebra associated with transformations (such as rotation) and these algebras must interwork correctly together.

• The first type of algebra defines how a given point is transformed, that is, a given rotation must define where every point, before the rotation, ends up after the rotation.
• The second type of algebra defines how rotations can be combined, that is, we first do 'rotation 1' then we do 'rotation 2' this must be equivalent to some combined rotation, say: 'rotation 3'.

The diagram on the left tries to illustrate this. The blue arrows, going from left to right, show different rotations which take a point Pin and moves it to point Pout. The red arrow, from top to bottom, takes two rotations and combines them to give a third.

We will see here how to use quaternions to do both of these algebras.

Summary of results

Rotating Points

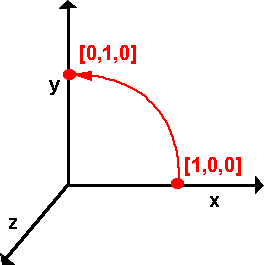
Probably the most important result on this page is the formula for representing rotations in 3 dimensions using quaternions (although we will also discuss how to use quaternions for other transforms on this page). This formula for 3D rotations is:

P_out = q * P_in * conj(q)

where:

• P_out and P_in are points in 3D space represented by the i, j and k parts of a quaternion (real part =0)
• conj() is a conjugate function explained on this page. We sometimes write conj(q) as q'.
• q is a quaternion which represents the rotation, if you prefer to think in terms of the angle and axis of the rotation then q is:

q = cos(a/2) + i ( x * sin(a/2)) + j (y * sin(a/2)) + k ( z * sin(a/2))

where:

• a = rotation angle
• x,y,z = rotation axis

So why is the rotation represented by this strange formula where the vector to be transformed is 'sandwiched' between two slightly different variants of 'q'? It is quite hard to get an intuitive grasp of this, although its easy to use it if you don't worry too much about how it works. If, like me, you like to know why things work then I have tried to work out an answer on this page.

Combining Rotations

The other important result is that a rotation of q1 followed by a rotation of q2 is equivalent to a single rotation of q2*q1. Note the reversal of order, that is, we put the first rotation on the right hand side of the multiplication.

The order worked out above assumes that each rotation, q1 and then q2 is done in the absolute frame of reference so we get q2*q1. When we are working in the frame of reference of a moving object such as an aircraft or spacecraft then the order is not reversed so the combined rotation is q1*q2.

absolute frame of reference	frame of reference of rotating object
q2*q1	q1*q2

where:

• q1 = first rotation
• q2 = second rotation

This makes it very easy to combine rotations so once we have expressed our rotational quantity as a quaternion it is easy to work with it.

Diagram Representation

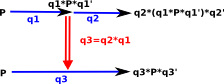We can now modify the diagram above to represent 'rotation 1' by a quaternion 'q1' and so on. 'P' represents any given point and the formulas, in black, show how that point is transformed.

Since we want the top and bottom arrows to represent the same rotation we require:

q2*(q1*P*q1')*q2' = q3*P*q3'

for all values of P. So we can see that:

q3=q2*q1

follows from the (sandwich product) formula for transforming a point.

Category Theory

We have now seen how the algebra for transforming points, and the algebra for combining transformations, are done. This may be all you need to do the calculations. The remainder of this page and the pages below it contain background information, proofs and theory. This stuff can be useful, because it hard to get an intuitive understanding of the topic but not everyone will need it.

Probably the most abstract way to approach this topic is category theory. For 'abstract' read hard but very powerful. Unless you know abstract mathematics (or program in Haskell) you may not know category theory, I have put some information about it here.

Options for Transform Equation

When we discussed complex numbers we saw that we could rotate by 90° by multiplying by 'i', this also works for quaternions but, as we shall show here, it does not work if we represent the rotation by a linear combination of 'i', 'j' and 'k'. So we need to find another way.

Imagine that we (incorrectly) represented a rotation by:

P_out = P_in * q

Where q is a quaternion representing the 3D rotation by a linear combination of 'i', 'j' and 'k'.

As discussed on the arithmetic page this can be represented by a multiplication table, which represents the equivalent matrix representation of the transform:

Pout.w Pout.x Pout.y Pout.z

=

q.w q.x q.y q.z q.x -q.w -q.z q.y q.y q.z -q.w -q.x q.z -q.y q.x -q.w

Pin.w Pin.x Pin.y Pin.z

We can compare this with the matrix representation of a 3D rotation and we can see that, although it works for pure values of 'i', 'j' and 'k' representing a rotation of 90 around each of the three planes, it does not work for a linear combination of them.

Order of multiplication is important for quaternions so instead of P_out = P_in * q lets try: P_out = q * P_in

Pout.w Pout.x Pout.y Pout.z

=

q.w q.x q.y q.z q.x -q.w q.z -q.y q.y -q.z -q.w q.x q.z q.y -q.x -q.w

Pin.w Pin.x Pin.y Pin.z

This does not work either so lets try both pre and post multiplying by the conjugate to give:

P_out = q * P_in * conj(q)

This matches the matrix representation of a 3D rotation so we use this 'sandwich' form: P_out = q * P_in * conj(q) to use a quaternion to apply a 3D rotation.

Note that because of this double multiplication 'i' now represents a 90° for each multiplication, that is, 90°+90°=180° and similarly for 'j' and 'k'.

Note also that the q.w²+q.x²+q.y²+q.z² in the top left element represents the scaling factor, if we want pure rotation without any scaling then, we normalise the quaternion that is:

q.w²+q.x²+q.y²+q.z² = 1

The Sandwich Product

In order to find how a point moves when being rotated in 3D we can use the 'sandwich product' as discussed on this page.

q * P_in * q^-1

or where q is normalised:

q * P_in * conj(q)

Is this something that is just specific to quaternions and this rotation question?

It turns out that it is more general than that, the 'sandwich product' can be used to represent many other types of transform… see geometric algebra, rotors conformal space and so on. But the 'sandwich product' is still more general than that, this form turns up in group theory and set theory, in this context it is known as a 'conjugacy' (not to be confused with the conjugate of a complex number or quaternion, here a conjugacy is the whole sandwich product).

So where does this function come from?

It results from two requirements:

• That there is an isomorphism (a kind of equivalence) between the quaternion group and the position of a point on a rotating object.
• The requirement that we can represent subsequent rotations by multiplying the quaternion

I turns out that this is the only mapping between quaternions and the position of a point on a rotating object is this sandwich product. this is explained for quaternions on this page and more generally on this page.

Why we use quaternions

Quaternions are very useful for calculating the results of rotations. On this page we discuss how a given quaternion can be used to rotate points in 3 dimensional space.

Although rotations in 3 dimensions have three degrees of freedom they are not a 3D vector space (we can't combine them using vector addition). Representations of 3D rotations using 3 scalar values are very messy, they are non linear, they have singularities and they are difficult to combine, see euler angle page for more details. To get round these problems we don't model the physical 3D space directly, instead we imbed it into a higher dimensional space, in this case the 4D quaternion space.

concept	3D space	4D space
position	x,y,z	p = 0 + i x + j y + k z
orientation	heading attitude bank	q = cos(a/2) + (i x + j y + k z)sin(a/2)
rotation	heading attitude bank	q = cos(a/2) + (i x + j y + k z)sin(a/2)
rotate a point	difficult to do	q * p * conj(q)
combine rotations	difficult to do	q1 * q2

Rotations are the most useful application of quaternions although we also discuss how to use them for other transforms associated with 2 dimensional planes in 3 dimensional space:

Type of transform	Formula to use
Rotation (around the origin)	Pout = q * Pin * conj(q)
Reflection in plane (through the origin):	Pout = q * Pin * q
Parallel component of plane:	Pout = ½ (Pin + q * Pin * q)
Perpendicular component of plane:	Pout = ½ (Pin - q * Pin * q)
Scaling:	Pout = scalar * Pin --- or combine with rotation or reflection
Translation:	Pout = q + Pin

Where:

• q = quaternion representing transform
• P_in = vector representing point before being transformed.
• P_out = vector representing point after being transformed.
• conj() = conjugate function.

Compound Operations

So it is possible to perform various types of transform using quaternions but can we combine them into a single operation?

We can for pure rotations, for instance if the first rotation is q1 we have:

x2 = q1 * x * q1'

we now apply a second rotation q2 to x2 giving:

x3 = q2 * (q1 * x * q1') * q2'

using the associative property of quaternions and the fact that (q2*q1)'=q1'* q2' (see conjugate function) then we get:

x3 = (q2*q1) * x * (q2*q1)'

So a rotation of q1 followed by a rotation of q2 is equivalent to a single rotation of q2*q1. Note the reversal of order, that is, we put the first rotation on the right hand side of the multiplication.

The order worked out above assumes that each rotation, q1 and then q2 is done in the absolute frame of reference so we get q2*q1.

When we are working in the frame of reference of a moving object such as an aircraft or spacecraft then the order is not reversed so the combined rotation is q1*q2.

The way that I am trying to understand this is when we are working in the frame of reference of the object then rotating the object is equivalent to keeping the object stationary and moving the frame of reference in the reverse direction (In tensor terms it is contravariant as opposed to covariant).

However if we want to include other types of transform so we have a combination of say rotations and translations then the above formulas contain both multiplication and addition then when we combine them then we can end up with very complex expressions.

This means that we cant necessarily derive a single quaternion that can represent a combination of the above transforms. This is obvious since a quaternion contains 4 scalar values so there is no way it can represent say the 6 degrees of freedom of a solid object.

If we want a single algebraic entity which can represent any combination of the above transforms then we would need to consider other algebras:

• Use matricies
• Use dual quaternions.
• Use projective or conformal projections.
• Use quaternions for the rotation part and handle the translation part separately (see affine translations).

If we want to rotate, reflect or scale around a point other than the origin, this is the same as doing the operation around the origin combined with a translation.

Converting the 3D vector into a quaternion

First we convert the 3D vector into a quaternion, to do this we set the imaginary parts of the quaternion to the x,y and z values of the vector, the real part of the quaternion is set to zero. This quaternion is therefore not normalised like the quaternion representing the rotation.

So we take the vector: (x,y,z)

And represent it by the quaternion: 0 + i x + j y + k z

Now we need to combine this quaternion, representing a point, with a quaternion 'q' representing the transform, this is calculated as follows:

Type of transform	Value of 'q'
Rotation:	q = cos(a/2) + i ( x * sin(a/2)) + j (y * sin(a/2)) + k ( z * sin(a/2)) where: a = rotation angle x,y,z = rotation axis
Reflection in plane:	q = i*x + j*y + k*z where: x,y,z = normal to plane
Parallel component of plane:
Perpendicular component of plane:
Scaling:	q = scalar

We then apply the appropriate formula from the following table to generate the output vector:

Type of transform	Formula to use
Rotation:	Pout = q * Pin * conj(q)
Reflection in plane:	Pout = q * Pin * q
Parallel component of plane:	Pout = ½ (Pin + q * Pin * q)
Perpendicular component of plane:	Pout = ½ (Pin - q * Pin * q)
Scaling:	Pout = scalar * Pin --- or combine with rotation or reflection

where:

• P_out = output point expressed as a quaternion
• q = quaternion representing the transform
• P_in = input point expressed as a quaternion
• conj() = conjugate function

If we apply this to every point in the 3D space we can think of the matrix as transforming the whole vector field.

If you just want to know how to use quaternions to do rotations in 3D space, that is all you need to know, you might like to look at some examples here. If you would like to know the theory behind it read on.

Examples

Here are some very simple examples, just to check that we are getting the expected results and we have not reversed a sign or anything like that.

To keep things very simple we will work with a plane represented by:
0 + 0 i + 0 j + 1 k
This represents the x-y plane in 3 dimensional space.

We can check what effect the different transforms have on a given point, say 0 + 2 i + 3 j + 4 k

Parallel component of plane

In this case we use the formula:

P_out = ½ (P_in + q * P_in * q)

Which gives:

P_out = ½ ((2 i + 3 j + 4 k) + k * (2 i + 3 j + 4 k) * k )
P_out = ½ ((2 i + 3 j + 4 k) + k * (-2 j + 3 i - 4 ))
P_out = ½ ((2 i + 3 j + 4 k) + 2 i + 3 j - 4 k
P_out = ½ (4 i + 6 j + 0 k)
P_out = 2 i + 3 j + 0 k

This is what we would expect when projecting onto the x-y plane, the x and y components stay the same and the z component is zero.

Perpendicular component of plane

In this case we use the formula:

P_out = ½ (P_in - q * P_in * q)

Which gives:

P_out = ½ ((2 i + 3 j + 4 k) - k * (2 i + 3 j + 4 k) * k )
P_out = ½ ((2 i + 3 j + 4 k) - k * (-2 j + 3 i - 4 ))
P_out = ½ ((2 i + 3 j + 4 k) - 2 i + 3 j - 4 k)
P_out = ½ (0 i + 0 j + 8 k)
P_out = 0 i + 0 j + 4 k

This is what we would expect when taking the parallel component to the x-y plane, the x and y components are set to zero and the z component is unchanged.

Reflection in plane

In this case we use the formula:

P_out = q * P_in * q
P_out = (k * (2 i + 3 j + 4 k) * k )
P_out = (k * (-2 j + 3 i - 4 ))
P_out = 2 i + 3 j - 4 k

This is what we want, the z plane is inverted, the other planes remain the same.

Mapping 3D coordinates to 2D coordinates in the plane.

It would be useful to be able to map between the 3D coordinates of points on a plane (using a quaternion) in 3D space and the corresponding 2D coordinates (using a complex number) within the plane.

We can do this using a 2×3 matrix (as described here), for example, but if we happen to be working with quaternions its a shame to have to switch to matrices.

An application of this would be projecting a 3D model onto a 2D computer screen or representing a 2D image in a 3D model.

I'm not sure if quaternions can do this? can anyone help?

Derivation of rotation formula.

I would like to derive the rotation formula from the formula for projecting onto planes, is this possible?

Equation for transforming a point

To calculate the resulting point (P2) when we translate the point (P1) using quaternions then we use one of the following equations:

For Reflection & scaling: P2=q * P1 * q

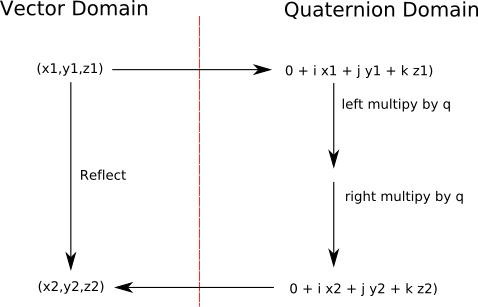
For Rotation & scaling: P2=q * P1 * q'

Where:

• P1 = original position of point in the following format 0 + i x + j y + k z
• P2 = resulting position of point after transform in the following format 0 + i x + j y + k z
• q = rotation quaternion = qw + i qx + j qy + k qz
• q' = conjugate of q = qw - i qx - j qy - k qz

In other words the elements are denoted by x, y and z for the position and qw, qx, qy and qz for the quaternion representing the transform.

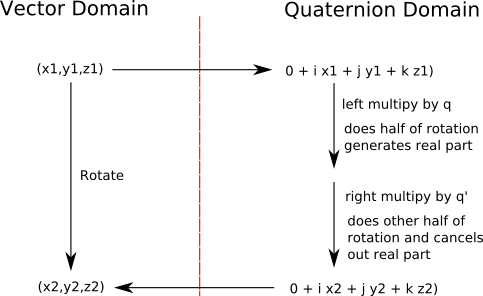
So why do these constructs work? Why does sandwiching a vector between two versions of the quaternion, that is transforming it, produce another vector which has been transformed in this way? I find it quite hard to get an intuitive interpretation of this, I can think of 3 approaches to this:

1. We need this double multiplication to do the rotation in two halves that cancels out the real part, enabling it to be converted back to a vector at the end, this is explained in more detail here.
2. The brute force method, we can show the above equations are correct by multiplying out all the terms and showing that they represent the same transforms as the matrix equivalents. The rotation case is proved below and the reflection case is proved on this page.
3. By deriving the rotation result by combining two reflections, see this page.

Combining Transforms

Combining Rotations

First combining two rotations 'a' and 'b', applying 'a' gives:

P2=a * P1 * a'

Then we apply 'b' to the result

P2=b * a * P1 * a' * b'

we can rearrange this by using (b*a)' = a' * b' which gives:

P2= (b*a) * P1 * (b*a)'

which is equivalent to a single rotation of (b*a). So a rotation of b*a is equivalent to rotating by a and then by b.

Combining Reflections

Combining two reflections should, in general, give a rotation. But can we multiply the quaternions representing these reflections to get the resulting rotation?

First combining two reflections 'c' and 'd', applying 'c' gives:

P2=c * P1 * c

Then we apply 'd' to the result

P2=d * c * P1 * c * d

Can we get the second part into the same form as the first? Well we could use (d*c)' = c' * d' which gives:

P2= (d*c) * P1 * (d'*c')'

Since c and d are reflections then the real part is zero so,

c' = -c

in other words, in the conjugate function we invert the imaginary part. So applying this gives:

P2= (d*c) * P1 * (d*c)'

so if we let q=d*c we have

P2= q * P1 * q'

note that, unlike c and d alone, q does have a real and imaginary part.

As explained on this page, the result of two reflections is a rotation. Its angle is twice the angle between the normals of the reflection planes. So the required rotation is twice:

q.x = (v1 x v2).x
q.y = (v1 x v2).y
q.z = (v1 x v2).z
q.w = | v1 | | v2 | + v1 • v2

double w; // real part of quaternion
double x; // imaginary i part of quaternion
double y; // imaginary j part of quaternion
double z; // imaginary k part of quaternion

sfvec3d transform(sfvec3d p1){
	sfvec3d p2 = new sfvec3f();
	p2.x = w*w*p1.x + 2*y*w*p1.z - 2*z*w*p1.y + x*x*p1.x + 2*y*x*p1.y + 2*z*x*p1.z - z*z*p1.x - y*y*p1.x;
	p2.y = 2*x*y*p1.x + y*y*p1.y + 2*z*y*p1.z + 2*w*z*p1.x - z*z*p1.y + w*w*p1.y - 2*x*w*p1.z - x*x*p1.y;
	p2.z = 2*x*z*p1.x + 2*y*z*p1.y + z*z*p1.z - 2*w*y*p1.x - y*y*p1.z + 2*w*x*p1.y - x*x*p1.z + w*w*p1.z;
	return p2;
}

EuclideanSpace

home

.