Collision in 2 dimensions (no rotation, no friction)
I am not sure how useful this case is? It would be quite difficult to arrange a collision where the objects are free to move in 2 dimensions but are prevented from rotation. However this is an intermediate case between collisions in one dimension and collisions in 2D with rotations, so it is useful to solve this to give ideas about how to proceed with the more complex case.
In the perfectly elastic case there are 4 unknowns (2 dimensions of velocity of object a + 2 dimensions of velocity of object b) and the conservation laws only give us 3 equations (conservation of momentum in 2 dimensions + conservation of scalar energy). Therefore the conservation laws are not enough to solve this.
In the perfectly inelastic case there are 2 unknowns (since the final velocity of both objects are the same we only have to find its component in the x and y dimention). Therefore the conservation of momentum alone should be enough to solve this.
Perfectly elastic (Conservation of energy)
|
Perfectly inelastic (Objects connect)
|
|
Final velocity of object a= = |
I am still working this out |  *  +  *  |
Final velocity of object b= = |
I am still working this out | * + * |
| impulse = | I am still working this out | (- )*  |
Perfectly inelastic case (Objects connect)
by conservation of momentum
va * Ma + vb * Mb = vf * (Ma + Mb)
where:
- va = initial velocity vector of object a
- Ma = mass of object a
- vb = initial velocity vector of object b
- Mb = mass of object b
- vf = final velocity vector of both objects
so
vf = * + *
impulse = change in momentum
therefore impulse on object a is:
i = (Va - Vf)*Ma
i = (Va - Va* +
Vb* )*Ma
i = (Va* +Va* - Va* +
Vb* )*Ma
i = (Va* +
Vb* )*Ma
i = (Va* +
Vb* )*Ma
i = (- )*
Perfectly elastic case (Conservation of energy)
First here is an attempt to solve using the conservation laws alone (conservation of energy and conservation of momentum).
Conservation of energy: 
* 
+ 
* 
= 
* + 
*
I cannot think of a way to represent conservation of energy using 2 dimensional vectors so I think its necessary to :
= 
+ 
i.e. by Pythagoras, square of
velocity is sum of x and y components
and: = 
+ 
and: = 
+ 
and: = 
+ 
this gives: * + * + * + * = * + * + * + *
conservation of momentum in x dimension: 
* + 
* = 
* + 
*
and conservation of momentum in
y dimension: 
* + 
* = 
* + 
*
We want to find the final velocities in x any y components so there are 4 unknowns
( , , and )
but there are only 3 equations, so we need more information before we can solve.
I guess this because the velocities will depend on where the objects collide. After all this is is the whole principle of snooker, pool, etc. If the queball hits on one side the object ball goes in the other direction. So we need to include some information about the collision point into the equations.
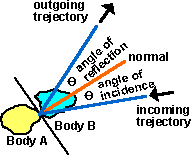
So we can try the same trick as in the one dimensional case and move to the frame of reference of body A, then body B will appear to bounce off it with minus the angle to the normal that it hit.
Therefore: ( - )
/ ( - )
= tan(2*theta)
To make things simpler, change the x-axis so that its along the normal and the y-axis so that its perpendicular to the collision:
so :
- = - ( - ) :the relative motion along the
normal is reversed.
and - = - :the
relative motion across the normal remains the same
from 2 : * + * = * + *
and * + * = * + *
rearranging gives: * = * + * - *
and * = * + * - *
substituting for in 4 gives: ( + - )* = * + * - *
and ( - + )* = * + * - *
* (+)
= * (- )+ *2*
and * (+)
= *( - )
= * 
+ * 
and = *
= + - = + * + *( -1)
= - + = * - +
= * 
- *
=- *
But these equations assume that the x-axis is along the normal and the y-axis is perpendicular to the collision. So for the general case we need to rotate the axis by theta.
Using conservation laws alone does not allow us to solve for the general case so we need to calculate the impulse as below:
