I don't think it’s possible to model a collision with 100% accuracy. The level of accuracy will depend on factors such as:
- Whether we model the deformation of the objects or whether we assume solid body collisions.
- What assumptions we make about elasticity coefficient and energy converted to heat.
- What assumptions we make about friction and how objects slide.
- How we handle multiple points of contact and simultaneous collisions.
There is no right answer to these questions, it depends on factors like: what we want to do, what accuracy do we need, how much computer power do we have, how stable must the simulation be and what type of materials are we dealing with.
I have been discussing these issues with Rahil Baber by email, who has written a program to simulate solid body collisions without friction and has reviewed other work on the subject.
First he has written a very useful survey of the subject which he has kindly allowed me to make available here: RigidBodySimulation.pdf. This document gives a very good introduction to the subject, includes the formulas for solid body collision response without friction, and outlines problems in writing a robust simulator. (Disclaimer: no claims are made about the accuracy of this document).
To help readers get a flavour of the types of issues they should be aware of, and some of the work being done in this area, I have summarised below some of the things that Rahil discussed in our emails.
Problems with Rigid Body Simulation
Angular Motion in 3D
In 2D a body’s rotational behaviour is encapsulated by the moment of inertia which is a single constant scalar quantity. In 3D the moment of inertia is replaced by the inertia tensor which is a 3x3 matrix. What’s worse is that it does not remain constant; it changes as the objects orientation changes. Due to this, even under no external forces, the motion is very different in 3D. You may want to look at that part of the survey to see the formulae you have to integrate to calculate a body’s motion in 3D. He said his initial simulations looked completely wrong and he couldn't work out why. It turned out that he had given the inertia tensor silly values (even though they appeared reasonable) and suggested that it may be worthwhile writing an algorithm to automatically calculate the inertia tensor of a given object assuming its mass is uniformly distributed.
Sinking and Jittering
Possibly the worst problem you’ll face is sinking and jittering of objects which are meant to be at rest on a surface. For instance a box resting on the floor under gravity, or for a tabletop example how about a billiard ball pushed against a cushion due to a continuous strong breeze. The problem arises because when you drop a ball it collides with the ground and rebounds then collides again and again and again... Each time it loses some energy and the maximum height it reaches after each collision decreases geometrically. In fact it makes infinite collisions because the height never reaches 0 just becomes 1/2 lets say of its previous height. Because the height decreases geometrically so does the time between collisions, say it takes 1/2 the time between each collision, then the time it takes to come to rest is 1 + 1/2 + 1/4 + 1/8 + 1/16 + .... = 2. Consequently the amount of time it takes to make those infinite collisions and come to rest is finite! This is a major problem for computers, as they cannot simulate infinite collisions in a finite time (for something as simple as a ball maybe they could because we analytically know the right answer, in general though we don't). Hence computers make approximations and the force it applies is either too weak and the object sinks into the ground or it is too large and the object vibrates on the surface of the ground. There are various workarounds but they just push the problem elsewhere, there's no real way to get rid of it entirely.
Resting Contacts
Usually the rigid body simulation algorithm will resemble:
- Move objects as if in free fall motion (ignoring collisions) for a small time step.
- Apply impulses if two objects are close/penetrating AND the approach velocity is positive (forgetting the latter part is a common mistake).
- Go to step 1.
Imagine a box resting on a table. The velocity of approach is 0, so no impulse is applied, and the box will intersect with the table, in the next time step. This leads to the box sinking through the table. You could argue well its ok because, in the time step after that, it will have some downward velocity, so an impulse will be applied, and the object will be given an upward velocity, which causes it to move out of the table. However what if e=0, then no impulse would be provided (or more accurately the impulse would have 0 magnitude), and the box would continue on its merry way through the table. This is perhaps a pathological example but it highlights the fact that you need to do something different when the contact is a “resting contact” i.e. when the approach velocity is 0 but the approach acceleration is positive. There are two popular methods of resolving resting contacts: the analytic force approach where you work out forces and numerically integrate them through time (see Baraff’s papers for more information), and the impulse approach where you replace forces by high frequency impulses (see Mirtich's thesis for more information).
Multiple Bodies
Striking a body which is in contact with a third body is a problem. There are two ways this could happen see p30 of my document both are correct which is another limitation of the rigidity condition.
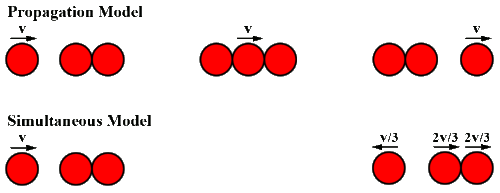
As an example of the issues: the above diagram shows the difference between the simultaneous and propagation model. In both cases energy is conserved, in each collision (e=1), but the outcome is very different depending on the assumptions made when colliding with bodies that are already in contact.
Friction
David Baraff in a paper (see literature section below) gave an example of a stick dragging along the ground and asked what the normal force should be to stop gravity making it penetrate into the ground. He cleverly set up the situation so that the larger the normal force the larger the frictional force (due to F = mu N), and the larger the frictional force the larger the angular acceleration pushing the stick into the ground and so the larger the normal force had to be to stop this, etc. So in fact this simple situation has no solution, just because we had added friction into the mix! This of course doesn't happen in real life because things aren't rigid, but it is an important limitation of this method. For perfect spheres friction isn't a problem as normal forces don't contribute to angular motion.
Brian Mirtich’s thesis highlights a problem with the jittering effect, and slopes, when you include friction. He notes that if a box is resting on a slope it won't slip if friction is high enough. However since simulations tend to have objects vibrating (usually at high frequency and amplitude less than a pixel in magnitude) that the box will momentarily be out of contact with the surface at various points and so the frictional force will vanish to 0 at those points. This results in the box slipping down the slope, which does not match what we’d expect to see. He also highlights a paper written by W. J. Stronge which shows that it is not valid to use Newton’s law of restitution when we do collisions with friction, as doing so may increase the energy of the system. This makes collisions with friction significantly more complicated.
Literature and People
The stick
dragging along the surface with no solution is in "Coping with
Friction for Non-penetrating Rigid Body Simulation" by David
Baraff (all his work is good, and fairly readable). He has another
paper called "Issues in Computing Contact Forces for
Non-Penetrating Rigid Bodies" which may be of interest but I
haven't read it. "Non-penetrating Rigid Body Simulation"
looks very readable. “Analytical Methods for Dynamic Simulation of
Non-penetrating Rigid Bodies” is a great introduction to analytic
force determination. Papers
by David Baraff. The
course notes on the site are a good resource for beginners.
The
other person whose work seems to have been quite influential is Brian
Mirtich (thesis
here).
His thesis is quite comprehensive on the area of rigid body
simulation (with friction). He has a different approach to Baraff.
Baraff tries to analytically work out the normal forces that occur
whereas Mirtich tries to handle the normal forces as a lot of high
frequency impulses.
Rahil Baber comments and a correction to Brian Mirtich paper as mentioned at the start of this page a lot of this comes from a very interesting email discussion with Rahil Baber. Rahil has now written this useful and interesting paper. In fact this might be a good starting point for further study as it summarizes the Brian Mirtich paper.
Rahil has also sent me his code for 2D collision with friction here. This code is written in C and uses OpenGL.


