Ways to specify a Line in 3D space
If a line goes through the origin we can specify it using a single vector but how do we specify a line that does not go though the origin?
Here are some possibilities:
- If the line is a finite length we can specify the endpoints of the line.
- If the line is of infinite length we can specify any two points on the line.
- Or we can specify one point on the line and the direction of the line.
These methods all require 2 vectors (6 scalar values) to specify the line.
The disadvantage of these methods is that they involve one or two arbitrary points. Therefore two identical lines may be specified differently and so we cant easily check if the lines are identical or how close they are to each other.
A better way to do this would be to use the direction of the line and the vector direction from the origin to the nearest point on the line to the origin.
A related way is to start with an arbitrary point on the line and take its cross product with the direction vector. This cross product is independent of the point chosen and uniquely defines the line which is what we are looking for. The direction vector along with this cross product are known as plücker coordinates and are denoted by:
(v ; P × v)
The semicolon ';' distinguishes it from a 6 dimensional vector.
where:
- v : unit vector (normalised to unit length)
- P × v : known as the 'moment' its direction is mutually perpendicular to both the vector and to the shortest distance between the origin and the line.
Plucker Coordinates From Direction and Point on Line
If the direction of the line is specified as follows:
- v
- direction vector.
- P
- point on line.
Then the plucker coordinates are defined as:
(v ; P × v)
where:
- × = vector cross product
- ( ... ; ... ) notation used to denote these two vectors represent plucker coordinates.
Plucker Coordinates From Endpoints of Line
If we have a line of finite length in 3 dimensions (known as a directed line) we can define the line by its endpoints, in this case 'p' and 'q'.
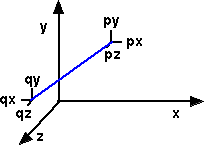
we can therefore define the line by the following 6 parameters:
[px,py,pz,qx,qy,qz]
However there are advantages to generating a different set of 6 parameters, known as plücker coordinates, as follows.
To convert these parameters to plücker coordinates we first calculate the direction vector which is the direction of 'p' from 'q' which is just the difference of the two vectors:
| px - qx |
| py - qy |
| pz - qz |
To get the second part of the plücker coordinates we take the cross product of this with P (we could have equally chosen q) to give:
| py*(pz - qz) - (py - qy)*pz |
| pz*(px - qx) - (pz - qz)*px |
| px*(py - qy) - (px - qx)*py |
which can be expanded to:
| py*pz - py*qz - py*pz + qy*pz |
| pz*px - pz*qx - pz*px + qz*px |
| px*py - px*qy - px*py + qx*py |
and canceling out gives :
| - py*qz + qy*pz |
| - pz*qx + qz*px |
| - px*qy + qx*py |
So the plücker coordinates are:
(px - qx, py - qy ,pz - qz ;qy*pz-py*qz ,qz*px-pz*qx, qx*py-px*qy)
Alternative notation
Some sources change the order as follows:
[px*qy - qx*py , px*qz - qx*pz , px - qx , py*qz - qy*pz , pz - qz , qy - py]
These are formed from the determinants of the 2x2 minors of the following matrix:
| px | py | pz | 1 |
| qx | qy | qz | 1 |
Side Operator
If we have two such lines, we can define a 'side operator' which relates the two lines 'a' and 'b' as follows:
side(a,b) = a[0]*b[4] + a[1]*b[5] + a[2]*b[3] + a[3]*b[2] + a[4]*b[0] + a[5]*b[1]
This is zero when the lines are parallel.
Intersecting Lines
If we have two lines, shown here in blue, which are not necessarily parallel or related to each other.
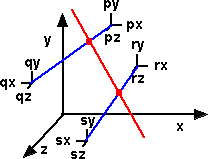
There are many possible lines, example shown in red, which intersect the two lines.
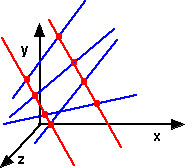
If we increase the number of lines to three there may still be many possible solutions. If we increase the number of lines to four there may be 2 solutions in the most general case. These solutions are given by a quadratic equation.
Example
Calculate the plücker coordinates of the following lines:
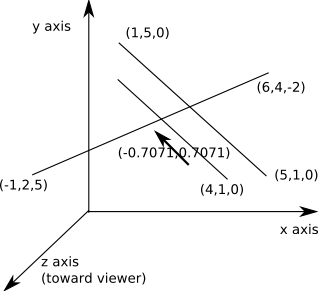
- A : A line form (5,1,0) to (1,5,0) with a rotation of 30° around the line (-0.7071,0.7071,0)
- B : A line through the point (4,1,0) in the direction (-0.7071,0.7071,0) with a rotation of 30° around the line (-0.7071,0.7071,0)
- C : A line form (-1,2,5) to (6,4,-2) with a rotation of 60° around the line (0,0.7071,0.7071)
Applications
One important application of plucker coordinates concerns the transform of a solid body in mechanics which may include both rotation and translation. This can be done using screw theory which often uses plucker coordinates to define the line of the screw.
