Rotation is a transform which preserves distances and angles (for an introduction see this page). Here we explore the issues when we extend this concept to higher dimensional spaces.
Why study rotations in high dimensional spaces?
In most cases 3D rotations are all that is needed to model rotations in the world around us. However there might be some situations where we might want to go to higher dimensions:
- Space-Time: What is the meaning of rotating between space and time dimensions? See the special relativity pages.
- Theoretical Physics: There are many theories (such as string theory) which propose higher dimensional spaces.
- Using a subset of higher dimensional space: It is quite difficult to combine rotation and translation transforms within the same model and to do this in a useful way we sometimes embed our space within a higher dimensional space. Examples are: Projective Space and Conformal Space which are useful when we are writing computer programs to do things like raytracing and game physics.
- Looking for patterns between higher dimensional spaces: Sometimes understanding the common features between rotations in different spaces gives us a better intuitive feel for the subject.
Finite Rotations
Here we are looking at finite rotations, continuous rotations like angular velocity can be combined using vector addition in any dimensional space.
As we move to higher dimensional spaces then calculating and combining finite rotations gets more complicated. In two dimensions we can either add angles or multiply complex numbers or equivalent matrices. When we move upto three dimensions combining rotations is no longer commutative. When we move to 4 and above dimensions then combining (basic) rotations no longer necessarily gives another (basic) rotation, instead we need to work in terms of compound rotations which contain the complete Clifford even subalgebra rather than just scalars and bivectors. (see Penrose book below P209).
Effect of higher dimensional spaces:
| 2D | 3D | 4D | nD | |
|---|---|---|---|---|
| combining rotations can be done in any order (transforms commute) | yes | no | no | no for n>2 |
| combining rotations gives another rotation | yes | yes | no | no for n>3 |
| degrees of freedom (basic rotation) | 1 | 3 | 6 | n*(n-1)/2 |
| degrees of freedom (compound rotations) | 1 | 3 | 7 | 2n/2 -1 |
The formula for the degrees of freedom for basic rotation comes from the number of combinations of k objects from n which is normally given by:
n!
----------
k!(n - k)!
So since rotations take place in a plane (i.e. two dimensions) we set k to 2 which gives:
n!
----------
2!(n - 2)!
which can be simplified to n*(n-1)/2
Types of Algebras:
There are two types of algebras that could be used:
| Matrices (tensors) | Clifford Even Subalgebras | |
|---|---|---|
| represent 2D rotation as: | 2×2 matrix where: [M][M]t=1 and det M =+1 |
complex numbers |
| represent 3D rotation as: | 3×3 matrix where: [M][M]t=1 and det M =+1 |
quaternions |
| represent 4D rotation as: | ? | scalar + 6 bivector terms (+ 1 quadvector for compound) (note: not octonons) |
| advantages: | people sometimes find them easier to understand | |
| transform point p | p' = [M]p | p' = r p r-1 where: r=scalar+bivector+(may have other even terms) |
| compound rotation | multiply matrices | multiply multivector |
Interpretation of Geometry of Rotation:
We can analyse rotation in different ways, each has its pros and cons, especially when we extend these concepts to higher dimensions.
In terms of axis of rotation.
Here we define the rotation in terms of what does not change, that is the axis it rotates around, people often find this the most intuitive to understand. In two dimensions this axis is just a point around which other points rotate, in three dimensions it is a vector, in four dimensions it is an oriented plane and so on, this is for basic rotations, compound rotations in 4D and above get a bit more messy. Although this is the most intuitive I cant think of a way to construct the transform equations from this starting point.
In terms of plane of rotation.
Here we define the rotation in terms of what does change, that is the two dimensional plane within which points move as they rotate. We can factor the rotation into the following steps:
- Move point along perpendicular line to the plane which goes through the origin.
- Do simple 2 dimensional rotation in the plane.
- Move point back along the perpendicular line to the same distance from the plane that it was originally.
This method seems to work best when using matrices: see this page for full working . I don't think this method will work properly for compound rotations in 4 dimensions and above since we need to take into account the quadvector and other even blades generated.
In terms of 2 (or an even number) of reflections.
We can represent a rotation as an even number of reflections (as explained on this page).
I tend to have an intuitive problem with this method on the grounds that I think of finite rotations as related to continuous rotations (as discussed here) so that they are related by differentiation. In these terms it is quite difficult to think of a finite rotation as a number of 'jumps' and it is tempting to think of this as just a curious relationship between different types of transform.
However, I think its worth overcoming these objections, because this method seems to provide the most powerful way to analyse rotations. This method works in any dimensional space, whether the dimensions square to +ve or -ve (provided the dimensions anticommute) and it works with basic rotations (2 reflections) and compound rotations (even number of reflections).
Reflection swaps the left and right-handedness of the object being reflected:
- reflection = odd number of orthogonal basis vectors reversed.
- rotation = even number of orthogonal basis vectors reversed.
So that is a reason that we need an even number of reflections.
This method works very well with Clifford algebras and explains why rotations are represented by even sub-algebras (more here).
The rotation angle produced by two mirrors depends on the angle between the two mirrors. There is a 2:1 ratio between the angle of rotation and the angle between the mirrors which applies, even when we move to higher dimensions, this allows us to relate this method to the spinor properties of rotations as described on this page.
In terms of exponential.
In two dimensions we have Euler's equation: r eiθ = r (cos(θ) + i sin(θ)). This relates the complex number and angle representation of the rotation. Explained on this page.
However this does not work very well in higher dimensional spaces, because in 3D and higher rotations are not commutative there is no way that we are going to combine rotations using addition, in fact in 3D the equivalent of Euler's equation becomes a much more complicated series known as the Baker-Campbell-Hausdorff formula. As explained here.
We will now look at how these approaches can be applied in different dimensional spaces.
Rotations in 1 dimension
In one dimension a point can only move along the dimension, there are not enough dimensions for rotation.
A point with no dimensions can't rotate, or if it did, there is no way for us to know its rotating. In physics we talk about fundamental particles having spin. If this spin is a physical rotation then the particle must have non-zero dimensions or we need a new mathematical system to describe it?
Rotations in 2 dimensions
In 2 dimensions there is only one way that an object can rotate, so rotation has one degree of freedom, represented by an angle.
Of course we can rotate around different points in the plane. However rotation around a point is equivalent to rotation around the origin combined with a linear movement.
An orientation in 2D might therefore be denoted by θ
The speed of a continuous rotation is usually denoted by omega: ω
which is dθ/dt.
The position of a point, on an object being rotated, can be given by the linear relationship:
x' = x*cos(θ) - y*sin(θ)
y' = x*sin(θ) + y*cos(θ)
where:
- x',y' = coordinates of point after rotation.
- x,y = coordinates of point before rotation.
If we use Clifford algebra then a 2D rotation is represented by the product of two 2D vectors (a e1 + b e2)(c e1 + d e2) which gives one scalar term and one bivector term (e12), this is equivalent (isomorphic to) complex numbers. Note the odd grades (vectors in this case) cancel out because the dimensions anticommute. More detail on this page).
Rotations in 3 dimensions
There is a lot of information on these pages about rotation in 3 dimensions as this is used for computer games.
There are 3 degrees of freedom for 3D rotations as discussed on this page. We can define a 3D rotation by an axis vector and an angle around that axis:
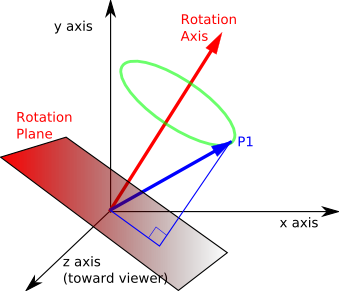
However this way of describing rotations is specific to rotations in 3 dimensions.
A more general way to define rotations is by defining a rotation plane. Points in the rotation plane remain in the plane when rotated.
The reason that the axis vector defines rotations in 3D is that in 3D each plane is related to a given line, planes and lines are duals, but only in 3D.
Continuous Rotations in 3D
The rate of rotation can be measured in each plane, for instance the rotation in the x-y plane can be written: ωxy . For continuous rotations we can represent as a linear combination of the rotations in each plane, it is represented as a vector space:
(ωyz, ωzx, ωxy)
This is a bivector (see 'directed area' box on right)
Because of the duality of planes and lines in 3D we could also represent each plane by the axis that it rotates round as follows:
(ωx, ωy, ωz)
This is the usual notation for 3D.
Finite Rotations in 3D
Finite rotations, or orientations, we cant represent as a vector space, instead we need to use matrix of quaternion algebra.
There are a number of ways that these can be calculated, possibilities are:
- Reflection in two planes at a given angle to each other.
- Project onto a plane, rotate, then project back.
In the second case, the matrix to map onto a plane (to get the parallel component to the plane) is:
|
|
we can rotate in a given plane as follows:
| x' y' z' |
= |
|
|
|
where:
- basis1 = (b1x,b1y,b1z) = 3D vector in plane of rotation toward initial position of point projected onto plane.
- basis2 = (b2x,b2y,b2z) = 3D vector in plane of rotation perpendicular to initial position of point.
- r = distance to point projected on to plane.
Example:
Rotation in x-z plane. In this case:
basis 1 = (1,0,0)
basis 2 = (0,0,1)
so:
| x' y' z' |
= |
|
|
|
multiplying matrices gives:
| x' y' z' |
= |
|
If we use Clifford algebra then a 3D rotation is represented by the product of two 3D vectors (a e1 + b e2 + c e3)(d e1 + e e2 + f e3) which gives one scalar term and three bivector terms (e12, e31 and e23), this is equivalent (isomorphic to) quaternions. Note the odd grades (vectors and trivectors) cancel out because the dimensions anticommute. More detail on this page).
Rotations in 4 dimensions
See Roger Penrose book (panel below) page 209.
If we use Clifford algebra (Which I find is the best way to investigate 4D and above rotations) then a 4D rotation is represented by the product of two 4D vectors (a e1 + b e2 + c e3 + d e4)(e e1 + f e2 + g e3 + h e4) which gives one scalar term and six bivector terms. However if we then go on to combine that with another rotation, that will be equivalent to 4 reflections, this means we may get an e1234 (quadvector term).
In general in 'n' dimensions we need to use the complete even subalgebra to represent any combination of rotations.
More detail on this page).
Note that this is not the same as octonons, as we explained here the algebras generated by the Cayley-Dickson doubling process diverge from the Clifford algebras in 4D and above.
