So far we have been looking at equations containing real numbers, in this section we will be looking at algebras where each element is a compound type made up of multiple quantities. In geometric terms each of these real quantities represents a dimension.
Most of these algebras are 'vector spaces over a field' this means that these algebras have at least two operations, addition and scalar multiplication defined as follows:
| operation | notation | explanation |
|---|---|---|
| addition | V(a+b) = V(a) + V(b) | the addition of two of these compound quantities is done by adding the corresponding elements of the two quantities. |
| scalar multiplication | V(s*a) = s * V(a) | a scalar product of a compound quantity is done by multiplying the scalar product with each of its terms individually. |
These operations interact according to the distributivity property:
s*(b+c)=s*b+s*c
This is what gives such algebras the linear property (see Euclidean space box on right)
There is also a more general family of algebras (less constrains) than 'vector spaces over a field' these are 'modules over a ring'.
In addition to the 'scalar' multiplication the families of algebras we are discussing will also have additional structure defined in terms of other multiplications which will give the individual algebras their flavor, for instance:
- Do dimensions square to positive or negative values (real or imaginary dimensions)?
- Do dimensions commute or anti-commute with each other?
If you are interested in a specific algebra such as vectors, complex numbers, quaternions and Clifford algebra then it is best to go directly to these topics now. Read this section if you want to investigate the common theory of these algebras.
One of the reasons for investigating this subject is to create a computer program which can work with different algebras and combine them in various ways, I am working on such a program, here.
To do this we will use the following approaches:
- Defining an algebra using a Cayley Table.
- Relating the Cayley table to algebraic properties such as commutative, associative, distributive, divisible, etc.
- Combining algebras by combining the individual Cayley tables. Application of Kronecker product and sum
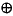 and
and  .
. - Spliting an algebra into subalgebras.
- Generating Clifford algebras and hyper-complex numbers by doubling up from simple 2 dimensional algebras.
Multi-Dimensional Algebra
Sometimes it makes sense to combine together a set of real numbers to form a single, indivisible entity, we can then use this entity in equations in the same way that we have used real number up to now. When we do this we need to be sure that we know the rules for working with these entities, the rules may possibly be different than when we are working with real numbers. Each algebra will also have its own rules for addition and/or multiplication and each will have its own notation. For more information see this page.
For such a precise subject the terminology in mathematics is difficult to tie down. It seems that when mathematitions extend the subject they tend to reinterpret what went before and we end up with overlapping terminology. I am trying to keep the terminology, on this site, consistent at much as I can: definitions on this page.
Vector Spaces
Vector spaces have at least one dimension that behaves like real algebra, known as a 'scalar' and it has simple rules for addition and scalar multiplication:
- (v1,w1) + (v2,w2) = (v1+v2 ,w1+w2)
- α(v,w) = (αv,αw)
That is: the rule for addition is that we add corresponding terms, for scalar multiplication: to multiplying the whole term by a scalar is equivalent to multiplying each element by the scalar.
In classical vector algebra the scalar is a separate quantity from the vector quantity and there are 3 types of multiplication defined:
- scalar multiplication: scalar×vector=vector
- dot multiplication: vector•vector=scalar
- cross multiplication: vector×vector=vector (only works in 3 & 7 dimensions).
K-Algebra
This is a vector space where there is a multiplication which can be applied to any terms and will always give a valid result (multiplication is closed). This result is determined by multiplying the basis elements.
Matrices
Matrices can represent any linear relationship. There is an isomorphism between certain matrices (orthogonal) and some hypercomplex algebras.
Hypercomplex Algebras
This is where the terminology is most vague 'Hypercomplex numbers' tends to be used for various generalisations of complex numbers. Here we will use 'hypercomplex' to represent algebras determine the product of two terms by:
(a ei)*(b ej) = a*b*Sij*(ei![]() ej)
ej)
where:
- a, b = the scalar values.
- Sij = represents the sign, it is a step function which is -1 or +1 depending on i and j.
- ei
 ej = represents the type given by the Kronecker product.
ej = represents the type given by the Kronecker product.
ei![]() ej will always be the same for an algebra of a given dimension and can easily be calculated, provided the elements are represented in bit order, by taking the bitwise exclusive or of the two operands.
ej will always be the same for an algebra of a given dimension and can easily be calculated, provided the elements are represented in bit order, by taking the bitwise exclusive or of the two operands.
So the nature of the entire algebra can be represented by Sijthe sign value of the product. For an 'n' dimensional algebra this can be shown by an n×n array of binary values. For a fuller explanation of this see this page.
The two most important examples of hypercomplex algebras are Clifford and Cayley-Dickson Algebras (which overlap to some extent) although there may be other hypercomplex algebras?
Clifford Algebras
In Clifford algebras the product of two different vector basis ei^ej cannot be simplified further and is left as it is as a bivector basis. In further multiplications we bay go on to generate trivector basis and so on.
More on Clifford algebras here.
Cayley-Dickson Algebras
In Cayley-Dickson algebras the product of two different vector basis ei^ej is represented as a new vector basis ek and in any further iterations is treated as just another vector basis. Converting bivectors to vectors at each stage explains why the algebraic properties of these algebras degrade every time we double up the dimension.
More on the Cayley-Dickson doubling process here.
Cayley Table
The Cayley Table is a good way to completely specify the multiplication rules of a multi-dimensional algebra. This allows us to easily lookup the result of multiplying any two elements of a given algebra. the result is made up of 3 parts:
- The scalar 'analogue' value of the result.
- Type of the result.
- Sign change of the result.
This assumes that the product of any two elements will be a single type which is the case for the simpler algebras that we are concerned with.
There are an infinite number of scalar values so we can't make a table from that but the type and sign can be combined into a table.
For more information see this page.
Terminology
We will be using the following notation on these pages:
| notation | meaning | basis | Alternative |
|---|---|---|---|
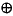 |
direct sum | ||
| ^ | exterior algebra | ||
| ^k | exterior algebra kth blade | ||
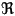 |
scalar | e0 | |
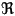 ² ² |
2 dimensional vector | e1,e2 | |
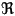 ³ ³ |
3 dimensional vector | e1,e2,e3 | |
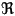 n n |
n dimensional vector | e1…en | |
^²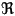 ² ² |
bivector based on 2D algebra | e12 | |
^² ³ ³ |
bivector based on 3D algebra | e12,e31,e23 | |
| C | complex numbers | 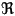   |
|
| H | quaternions | 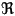 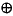 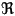 ³ ³ |
|
| O | octonions | 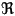   7 7 |
|
For more information about the maths notation on this site see this page.