On this page we will look at various ways that we can use Geometric Algebra (GA), based on 3D vectors, to represent transforms such as rotation and reflections.
We will start with pure rotations using a conventional algebra where both the vectors square to +ve. This is just a 3 dimensional version of the more general rotation formula on this page.
We could just as easily use quaternions to to the same thing, however it is useful to show that in 3D multivectors can be equivalent to quaternions.
On this page we derived the following table summarises general transforms in any number of dimensions, here we will look at the specifics of this in three dimensions,
| derivation | transform | |
|---|---|---|
| no change | P/P=1 | (Va * P) / P |
| parallel component | go here | (Va • P) / P |
| perpendicular component | go here | (Va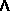 P) / P P) / P |
| reflection | go here | -(P * Va) / P |
| rotation | go here | (M * Va) / M |
| scaling | Va * s | |
| translation | ? | |
| intersections an unions | ? |
Notes:
- Here I have shown the inverse as "/P" because the order is not ambigous but if there is any doubt it is better to use P-1.
- Va is the input vector
- P is the transform vector
- M is the transform multivector (even grades)
- These transforms are all symmetrical around the origin, we are not yet introducing translations.
Reflections
Lets start with very specific cases, such as how the basis vectors are transformed, this will explain the basic principles we can then go on to the more general case.
then:
- The basis vectors are e1, e2, e3
- e1e1 = e2e2 = e3e3 = +1 (assuming space vectors square to +1)
- ei ej = -ej ei (vectors anti-commute)
So, first, how are the basis vectors transformed individually?
Let n = e1 = normal to mirror (so plane containing e2 and e3 contains mirror)
So the basis vectors transformed by the mirror as follows:
e1' = -e1 e1 e1 = -e1
e2' = -e1 e2 e1 = +e2 e1 e1= +e2
e3' = -e1 e3 e1 = +e3 e1 e1= +e3
So as we would expect, components of vectors parallel to the mirror are unchanged, components of vectors perpendicular to the mirror are inverted.
Now for the more general case, the normal to the first mirror is:
(a e1 + b e2 + c e3)
so e1 transforms to:
e1 -> -(a e1 + b e2 + c e3) e1 (a e1 + b e2 + c e3)
= -(a + b e2 e1 + c e3e1) (a e1 + b e2 + c e3)
= (b² + c² - a²)e1 -2 a b e2 - 2 a c e3
so e2 transforms to:
e2 -> -(a e1 + b e2 + c e3) e2 (a e1 + b e2 + c e3)
= -(a e1e2 + b + c e3e2) (a e1 + b e2)
= (-b² + c² + a²)e1 -2 a b e2 - 2 b c e3
so e3 transforms to:
e3 -> -(a e1 + b e2 + c e3) e3 (a e1 + b e2 + c e3)
= -(a e1e2 + b e2e3 + c) (a e1 + b e2)
= (b² - c² + a²)e1 -2 a c e2 - 2 b c e3
To represent a general rehich is the same result as the matrix:
| p -> |
|
[p] |
Reflections in 3D non-Eulidean space
So now lets look at how reflections act in non-euclidean spaces, in this case we must use the -P*Va*P-1 form, so if for instance e1² = e2² = -1, e3² = +1 then we get:
e1' = -e1 e1 e1-1 = e1-1 = e1 /(e1*e1)=-e1
| type | P direction |
Va point being reflected |
Result |
|---|---|---|---|
| e1²=+1 e2²=+1 e3²=+1 |
e1 | e1 | -e1 |
| e1 | e2 | e2 | |
| e1 | e3 | e3 | |
| a e1 + b e2 + c e3 | e1 | (b² + c² - a²)e1 -2 a b e2 - 2 a c e3 | |
| a e1 + b e2 + c e3 | e2 | (-b² + c² + a²)e1 -2 a b e2 - 2 b c e3 | |
| a e1 + b e2 + c e3 | e3 | (b² - c² + a²)e1 -2 a c e2 - 2 b c e3 | |
| e1²=-1 e2²=-1 e3²=-1 |
as above | ||
| e1²=±1 e2²=±1 e3²=±1 |
as above | ||
So to summarise the results:
- The reflections reverse one basis vector.
- The results are independant of whether the basis vectors square to +ve or -ve. (provided we use the -P*Va*P-1 form)
- The results work for a linear combination of basis vectors to represent a reflection in any line through the origin.
Representing 3D rotations
As we derived here the mapping to rotate the point 'p' is:
p' = M * p * M-1
Where:
M = is a multivector representing the product of two vectors and so contains only the scalar and bivector terms (even subalgebra) it is equivalent to (isomorphic to) quaternion algebra. we can show this as follows:
(a e1 + b e2 + c e3)(d e1 + e e2 + f e3) = (ad+be+cf) +
(ae-bd) e12 + (cd-af) e31 + (bf-be) e23
As we did with reflection we can see how are the basis vectors transformed individually and then the general case.
So, assuming e1e1 = e2e2 = e3e3 = +1, the basis vectors transformed by the scalar 's' and bivector e12 individually as follows:
rotation in pure scalar:
e1' = s e1 s-1 = e1
e2' = s e2 s-1 = e2
e3' = s e3 s-1 = e3
which is a null rotation.
rotation in pure bivector:
e1' = e12 e1 e12-1 = -e21e1e21 = -e1
e2' = e12 e2 e12-1 = e1e2e1 = -e2
e3' = e12 e3 e12-1 = e3e12e21 = +e3
So we can see that rotation reverses an even number of basis vectors and therefore does not alter left or right-handedness as we would expect.
For the more general case, the normal to the first mirror is:
(a + b e12 + c e31 + d e23)
and the normal to the second mirror is:
(a + b e12 + c e31 + d e23)-1 = (a - b e12 - c e31 - d e23) provided that the normal is normalised.
so e1 transforms to:
e1 -> (a + b e12 + c e31 + d e23) e1 (a + b e12 + c e31 + d e23)-1
= (a² + b² - c ² - d²) e1 + 2(ab-ac) e2 + 2(ac+bc)e3
so e2 transforms to:
e2 -> (a + b e12 + c e31 + d e23) e2 (a + b e12 + c e31 + d e23)-1
= (a² - b² + c ² - d²) e2+ 2(ab+ac) e1 + 2(ac-bc)e3
so e3 transforms to:
e3 -> (a + b e12 + c e31 + d e23) e3 (a + b e12 + c e31 + d e23)-1
= (a² - b² - c ² + d²) e3+ 2(ac-bc) e1 + 2(bc+ac)e2
which is equivalent to the quaternion to matrix:
| [R] = |
|
Representing 3D rotations
On this page we saw that we can use the 'sandwich' product to execute a transform as follows:
Pout = M Pin M-1
where:
- M = a multivector which defines the transform
- Pin = an object to be transformed, for example, a point.
- M-1 = the multiplicative inverse
- Pout = the result of the transform
A 3D rotation is represented by the product of two 3D vectors (a e1 + b e2 + c e3)(d e1 + e e2 + f e3) which gives one scalar term and three bivector terms (e12, e31 and e23), this is equivalent (isomorphic to) quaternions. Note the odd grades (vectors and trivectors) cancel out because the dimensions anticommute
In 3D we can greatly simplify this because the multiplicative inverse is equivalent to the reverse (described on this page). This is because there are only 3 basis vectors so we can't have two completely independent bivectors.
In other words M-1 = M† ,so ,
Pout = M Pin M†
where:
- M† = the reversal of the transform, that is we reverse the order of basis vectors in each term separately.
In this case M is a linear combination of the scalar and bivector terms:
Representing 3D transforms
To represent isometry transforms in 3D we need 3 or 4 scalar values (quaternion or 3D vector) to represent rotations and we need 3 scalar values (a 3D vector) to represent translation. A multivector based on 3D vectors therefore has enough values to represent 3D isometries , for instance (e12,e31,e23) might hold the rotation value and (e1,e2,e3) hold the translation value, but does the algebra work out? Can we do useful operations on the multivector using such a notation? Below I have shown how 3D multivectors can be used to implement reflections, rotations and scaling about the origin. However I cant find a way to represent a translation combined with these.
multivector = scalar part of quaternion + vector representing translation + bivector part of quaternion.
Of course we can represent a translation by adding a vector but what we are trying to do here is to combine rotation and translation into one multiplication operation. I cant find a way to do that here using 3D transforms, 3D transforms only seem to be able to do the same things as quaternions but not more.
To represent 3D rotations and translations with a single multiplication we need to goto a 4-dimentional algebra G 3,0,1 as described on this page.
Reflection Transforms
We can specify a transform by mapping a -> -n*a*n
In this section we will investigate the properties of such a transformation and show that if 'n' is a vector representing a normal to a plane then this expression represents a reflection in this plane. This can be derived by splitting the vector into components parallel and perpendicular to the plane but it still does not seem very intuitive.
-n*a*n
where:
- n = pure vector (multivector which contains only grade 1 terms - e1, e2 and e3)
- a = input multivector
- * = geometric product
Reflecting a vector
One reflection is given by:
p' = -n p n
where:
- p = vector being reflected
- n = unit vector which is normal to the mirror (plane in which p is reflected)
lf we are working in 3D Euclidean space then:
1) the basis vectors are e1, e2 and e3
2) e1e1 = e2e2 = e3e3 = +1 (assuming space vectors square to +1 !)
3) ei ej = -ej ei (all vectors anti-commute)
Let n = e1 = normal to mirror (so mirror is in e2^e3 plane)
So how are the basis vectors transformed by the mirror?
e1' = -e1 e1 e1 = -e1
e2' = -e1 e2 e1 = +e2 e1 e1= +e2
e3' = -e1 e3 e1 = +e3 e1 e1= +e3
So as we would expect, components of vectors parallel to the mirror are unchanged, components of vectors perpendicular to the mirror are inverted.
Reflecting a multivector
Expanding out the terms gives:
out.e= ( -n.e1*n.e1 -n.e2*n.e2 -n.e3*n.e3)*a.e
out.e1= (-n.e1*n.e1 +n.e2*n.e2 +n.e3*n.e3)*a.e1 - ( 2*n.e1*n.e2)*a.e2 - ( 2*n.e1*n.e3)*a.e3
out.e2= ( -2*n.e1*n.e2)*a.e1 +(n.e1*n.e1 - n.e2*n.e2 + n.e3*n.e3)*a.e2 - ( 2*n.e2*n.e3)*a.e3
out.e3= ( -2*n.e1*n.e3)*a.e1 - ( 2*n.e2*n.e3)*a.e2 +(n.e1*n.e1 n.e2*n.e2 - n.e3*n.e3)*a.e3
out.e12= (n.e1*n.e1 + n.e2*n.e2 - n.e3*n.e3)*a.e12 -( 2*n.e2*n.e3)*a.e31 -( 2*n.e1*n.e3)*a.e23
out.e31= ( -2*n.e2*n.e3)*a.e12 +(n.e1*n.e1 - n.e2*n.e2 + n.e3*n.e3)*a.e31 -( 2*n.e1*n.e2)*a.e23
out.e23= ( -2*n.e1*n.e3)*a.e12 - ( 2*n.e1*n.e2)*a.e31 +(-n.e1*n.e1 +n.e2*n.e2 +n.e3*n.e3)*a.e23
out.e123= -(n.e1*n.e1 +n.e2*n.e2 +n.e3*n.e3)*a.e123
This has interesting properties:
- The grade 0 output is dependant only the grade 0 input (out.e is a function of a.e)
- The grade 1 output is dependant only the grade 1 input (out.e1,out.e2,out.e2 is a function of a.e1,a.e2,a.e3)
- The grade 2 output is dependant only the grade 2 input (out.e12,out.e23,out.e23 is a function of a.e12,a.e23,a.e23)
- The grade 3 output is dependant only the grade 3 input (out.e123 is a function of a.e123)
since n is a unit length normal to the plane then: n.e1*n.e1 +n.e2*n.e2 +n.e3*n.e3 = 1
so,
out.e= -a.e
out.e123= -a.e123
The pseudoscalar is related to the determinant of a determinant of a matrix so it is not surprising that any reflection inverts it.
If the input is a vector then the output is:
out.e1= (-n.e1*n.e1 +n.e2*n.e2 +n.e3*n.e3)*a.e1 - ( 2*n.e1*n.e2)*a.e2 - ( 2*n.e1*n.e3)*a.e3
out.e2= ( -2*n.e1*n.e2)*a.e1 +(n.e1*n.e1 - n.e2*n.e2 + n.e3*n.e3)*a.e2 - ( 2*n.e2*n.e3)*a.e3
out.e3= ( -2*n.e1*n.e3)*a.e1 - ( 2*n.e2*n.e3)*a.e2 +(n.e1*n.e1 n.e2*n.e2 - n.e3*n.e3)*a.e3
Which agrees with the reflection expression derived on this page.
Rotations
Rotating a vector
Two reflections are given by applying this twice:
p' = n2 n1 p n1 n2
where:
- n2 n1 = unit bivector (even grade)
- n1 n2 = inverse (reverse) of unit bivector
So this is the rotation sandwich product.
We could keep repeating this to give trivectors, quadvectors... but only even grades will be free of reflections.
So now lets reflect in e1 followed by e2, which should give a 180° rotation,
how are the basis vectors transformed by the two mirrors?
e1' = e2 e1 e1 e1 e2 = -e1
e2' = e2 e1 e2 e1 e2 = -e2
e3' = e2 e1 e3 e1 e2 = +e3
Both e1 and e2 are inverted which is what we would expect if we rotate 180° around e3.
Now for the more general case, the normal to the first mirror is:
(a e1 + b e2 + c e3)
and the normal to the second mirror is:
(d e1 + e e2 + f e3)
so the spinor is:
(a e1 + b e2 + c e3)(d e1 + e e2 + f e3)
= a*d + b*e + c*f + (a*e - b*d)e1e2 + (b*f - c*e)e2e3+ (c*d - a*f)e3e1
= even Clifford![]() quaternion in 3D case
quaternion in 3D case
Rotating a multivector
We can form a rotation by combing two reflections as described on this page. So reflecting in plane 'n' gives:
-n*a*n
If we then reflect the result in a different plane 'm' we get the expression for the rotation:
m*n*a*n*m
but, since n and m are pure vectors, if we let
R = m * n
then
R† = n† * m†
but since n and m are pure vectors then n†= n and m†= m which means that:
R† = n * m
Which means that the expression for the rotation is:
R a R†
where R is known as a Rotor, since it is the geometric product of two pure vectors (multivectors containing only grade 1 factors) then the result is a multivector with only real and bivector (grade 0 and 2) parts. The real part comes from the inner product and the bivector part comes from the outer product.
We can expand out the terms of R a R† to give:

