Abstract
This page is about how geometric algebra can represent objects in two dimensions and some useful concepts for analysing 2D geometry.
To see how the same concepts can be described using more conventional vector algebra see this page.
This page assumes an understanding of coordinate systems described here, you may also want to review angles.
Points and Lines from the Origin
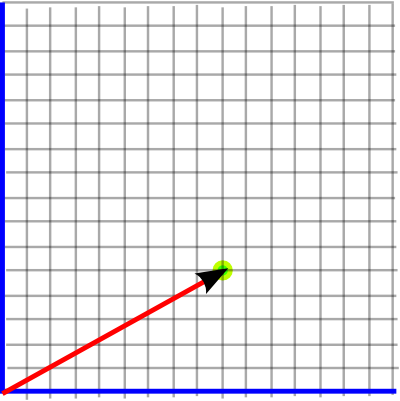
We can use a 2 dimensional vector to represent a displacement from the origin and therefore specify a given point by showing its displacement from the origin. For instance, the point shown below is 5 up and 9 right, which can be represented by the vector (9,5). By convention the x coordinate is shown first, then the y coordinate.
Angles
In two dimensions angles are scalar quantities.

If we have two 2D vectors (V1 and V2) then we could work out the angle between them, at the origin, by using:
angle = acos(real(v1*v2))
where:
- real() = function which returns the scalar component and sets e1, e2 and e12 components to zero.
- v1 = vector (scalar and e12 components are zero)
- v2 = vector (scalar and e12 components are zero)
- * = geometric product (see this page for definition)
or
angle = atan2(v2.y,v2.x) - atan2(v1.y,v1.x)
depending on whether we want to make the angle negative if V1 and V2 are swapped over. This is more fully explained on this page.
The first version uses the vector dot product '•' which generates a scalar from two vectors as explained here. The second version uses the x and y components of the vectors.
If we want to work out an angle at a point other than the origin, then we can translate the point to the origin by subtracting the displacement from all the vectors.
Areas
In two dimensions areas are scalar quantities. An area can be represented by one number, this does not say anything about the shape of the two dimensional object just the amount of 'surface' it contains.
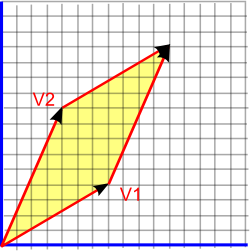
Any two dimensional closed shape encloses an area, this might be a simple shape like a rectangle or a circle or it could be a very complex shape. In any case its area is a single scalar number.
As an example let us take the area enclosed by two vectors as shown in yellow in the diagram above, this area is given by:
area = psudoScalar(v1 * v2)
where:
- psudoScalar() = function which returns the e12 component and sets scalar, e1 and e2 components to zero.
- v1 = vector (scalar and e12 components are zero)
- v2 = vector (scalar and e12 components are zero)
- * = geometric product (see this page for definition)
This is the green area in the diagram below:
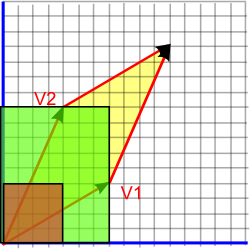
Any idea how I can show, geometrically using these diagrams, green area is the same as the yellow area?
Where next
To see how these objects can be projected onto other objects read this page.
To extend these ideas to three dimensions see this page.
