A 4D rotation is represented by the product of two 4D vectors (a e1 + b e2 + c e3 + d e4)(e e1 + f e2 + g e3 + h e4) which gives one scalar term and six bivector terms. However if we then go on to combine that with another rotation, that will be equivalent to 4 reflections, this means we may get an e1234 (quadvector term).
In general in 'n' dimensions we need to use the complete even subalgebra to represent any combination of rotations.
Note that this is not the same as octonons, as we explained here the algebras generated by the Cayley-Dickson doubling process diverge from the Clifford algebras in 4D and above.
Representing 3D transforms
To represent isometry transforms in 3D we need 3 or 4 scalar values (quaternion or 3D vector) to represent rotations and we need 3 scalar values (a 3D vector) to represent translation. A multivector based on 3D vectors therefore has enough values to represent 3D isometries , for instance (e12,e31,e23) might hold the rotation value and (e1,e2,e3) hold the translation value, but does the algebra work out? Can we do useful operations on the multivector using such a notation? I cant find a way to represent a combined translation and rotation with these.
We need to use a Geometric Algebra based on a 4 dimentional vector space G 3,0,1 to do what we want.
3D Rotation and Translation Using G 3,0,1 (Dual Quaternion)
This can be used to represent the group of spatial displacements in three dimensions SE(3) which can be used to represent a combination of 3D rotation and displacement. If you would prefer to do this using Dual Quaternion Notation see this page.
The G 3,0,1 or Dual Quaternion algebra can model the movement of a solid object in 3D, which can rotate and translate without changing shape, that is distances and angles between points on the object are preseved. In mathematical terms it can be used to represent the group of spatial displacements SE(3). The advantage of this is that we can represent a combined rotation with displacement operation with one multiplication operation.
There are 8 elements, the 4 quaternion elements (e, e12, e31 and e23) and their duals (e1234, e43, e42 and e41). This gives G 3,0,1 algebra represented by an 8x8 multiplication table as shown here:
a*b |
b.e | b.e12 | b.e31 | b.e23 | b.e41 | b.e42 | b.e43 | b.e1234 |
| a.e | e | e12 | e31 | e23 | e41 | e42 | e43 | e1234 |
| a.e12 | e12 | -1 | e23 | -e31 | -e42 | e41 | -e1234 | e43 |
| a.e31 | e31 | -e23 | -1 | e12 | e43 | -e1234 | -e41 | e42 |
| a.e23 | e23 | e31 | -e12 | -1 | -e1234 | -e43 | e42 | e41 |
| a.e41 | e41 | e42 | -e43 | e1234 | 0 | 0 | 0 | 0 |
| a.e42 | e42 | -e41 | -e1234 | e43 | 0 | 0 | 0 | 0 |
| a.e43 | e43 | -e1234 | e41 | -e42 | 0 | 0 | 0 | 0 |
| a.e1234 | e1234 | e43 | e42 | e41 | 0 | 0 | 0 | 0 |
Representing Transforms
The advantage of this is that we can represent a combined rotation with displacement operation with one multiplication operation.
- The e, e12, e31 and e23 terms together can represent rotation (as a normalised quaternion).
- The e1234, e43, e42 and e41 terms together can represent displacement (where e1234 =0 and (e43, e42, e41) is a vector equal to half the displacement)
We will do the transform using the same equation as we used for quaternion rotation:
P2=M * P1 * M'
where:
- P1 = vector representing the initial position of a point being transformed.
- M = the multivector representing the transform
- M' = the reversal of the multivector.
- p2 = the result which is a vector representing the final position of the point.
Pure Displacement (no rotation)
Let
- h = a 3D vector (x e41 + y e42 + z e43) representing half the displacement
- p1 = a 3D vector (x e41 + y e42 + z e43) representing the initial position of a point
The transform can be done by:
Pout = M * Pin * M †
(e + p2) = (e + h)(e + p1)(e + h)
= (e + h + p1)(e + h)
since (x e41 + y e42 + z e43)²=0 we can ignore these terms
= (e + h + h + p1)
= (e + 2 h + p1)
So this adds the dispacement (2*half) to the original point which is what we want.
If the rotation is 0 degrees, the rotation part is represented by:
(e + 0 e41 + 0 e42 + 0 e43), in other words e.
Example
So if we are initially at point (x=3, y=4, z=5) this will be represented by the multivector:
P1 = e + 3 e41 + 4 e42 + 5 e43
A pure displacement will be represented by the multivector:
(e + x/2 e41 + y/2 e42 + z/2 e43)
We now want to displace the initial point by (x=4, y=2, z=6) this will be represented by the multivector:
q = (e + 2 e41 + 1 e42 + 3 e43)
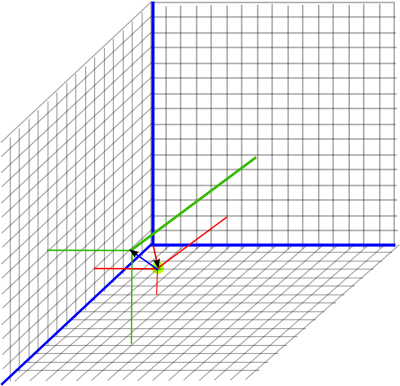
So to combine these, to give the resulting position, we use P2 = q * P1 * q' to give:
p2 = (e + 2 e41 + 1 e42 + 3 e43)*(e + 3 e41 + 4 e42 + 5 e43)* (e + 2 e41 + 1 e42 + 3 e43)
multiplying out the first two terms using the above multiplication table we get:
P2 = (e + 5 e41 + 5 e42 + 8 e43)*(e + 2 e41 + 1 e42 + 3 e43)
P2 = (e + 7 e41 + 6 e42 + 11 e43)
Pure Rotation (no displacement)
If the displacement is zero then e41 = e42 = e43 = 0 and the rotation is represented by the normalised quaternion as explained on this page.
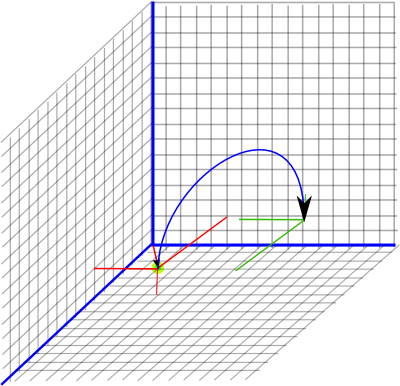
Example
Applying a rotation of point (3,4,5) by 180° around the x axis is given by:
P2 = (0 e+ e12)*(e + 3 e41 + 4 e42 + 5 e43)*(0 e - e12)
P2 = ( e12 - 3e42 -5e1234 + 4e41)*( - e12)
P2 = e - 3e41 - 4e42 + 5e43
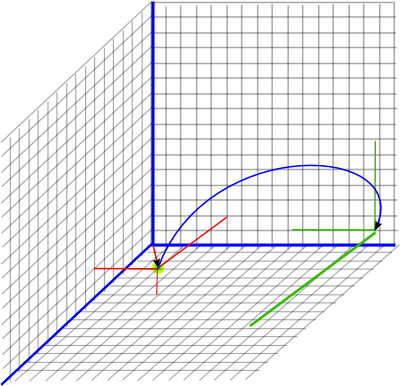
Combined Displacement and Rotation (displace then rotation)
Example
Starting from the previous position: (e + 3 e41 + 4 e42 + 5 e43)
and both displace by (x=4, y=2, z=6) and applying a rotation of 180° around the x axis represented by: (e12)
Therefore:
Q = (0 e + e12) (e + 2 e41 + 1 e42 + 3 e43)
Q = (e12 - 2 e41 -3 e42 + 1 e43)
So applying the transform gives:
P2 = (e12 - 2 e41 -3 e42 + 1 e43)*(e + 3 e41 + 4 e42 + 5 e43)*(e12 - 2 e41 -3 e42 + 1 e43)
P2 = (e12 -5 e41 -8 e42 + 5 e43)*(-e12 + 2 e1234 -3 e42 + 1 e43)
P2 = (e + 7e41 -6 e42 -11 e43)
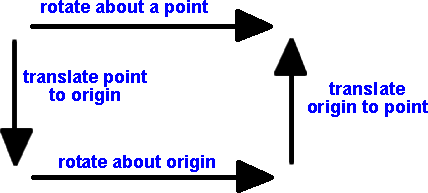
Rotation about a point
In the above we are rotating about the origin. This is sometimes what we want to do, for instance, if we are observing the world from the frame of reference of a car and we assume it to be at the origin then, when it turns, the other cars will appear to rotate round it. If we want a car to rotate about its own centre then we can just multiply the complex number part (e and e12) and ignore the e and ie part.
If we want to rotate about an arbitrary point then we first translate this point to the origin, then rotate about the origin, then translate the origin back to the point (as discussed on this page).
Combining Transforms
Pure Rotation
M = r
Pure Translation
M = e + ½t
Rotation then Translation
M = (e + ½t)*r
= r + ½t r
Translation then Rotation
Q = r*(e + ½t)
= r + ½r t
Rotation about a point
Q = (e + ½c)*r*(e - ½c)
= (e + ½c)*(e - ½r c)
= r - ½r c + ½c r
Inverse of Transform
To invert the multivector 'r' we use its reversal 'r†', to invert the translation 't' we use '-t'. With combined transforms we must also reverse the order that they are combined (don't forget that order is important for translations and their corresponding multivector).
The inverse of common transforms are:
| M | M-1 | |
| Pure Rotation | r | r† |
| Pure Translation | 1 + ε½t | 1 - ε½t |
| Rotation then Translation | r + ε½t r | r† - ε½r† t |
| Translation then Rotation | r + ε½r t | r† - ε½t r† |
| Rotation about a point 'c' | r - ε½r c + ε½c r | r† + ε½r† c - ε½c r† |
Equivalence to Dual Quaternion
The dimensions are related as follows:
G+ 3,0,1 |
dual quaternion |
| e | 1 |
| e12 | i |
| e31 | j |
| e23 | k |
| e41 | kε |
| e42 | jε |
| e43 | iε |
| e1234 | 1ε |
Use for Physics
The reason for taking this approach is to combine linear and rotational movement into a single transform and to automatically handle the interaction between them. It would be good to be able to use this algebra to work with physics equations. For instance, imagine we have a set of forces acting on a solid body, can we determine the linear and rotational movement by using dual quaternions?
G+3,0,1 represents both the linear and rotational movement as bivectors which are associated with planes, or quantities associated with them like rotations, we would expect a linier displacement to be represented by a vector. I think this issue could be a problem if we try to formulate the physics equations in terms of dual quaternions.
However linier movement can be represented as a rotation... If we rotate around a point at infinity! One way to handle this type of situation would be to use projective space as explained on this page. Is it possible to use this to do what we want? I would appreciate any help.

