Particle types
There are 2 types of particles, fermions which make matter and bosons which
make forces.
Fermions
Fermions are particles which make matter, they all have a spin
which is an 1/2 integer.
The types are shown in this table, antimatter is the same but with inverse
charge.
The quarks (top two in table) are in nucleus. The leptons (bottom two in table)
are outside nucleus.
| type |
electric charge |
weak charge |
strong charge |
gravity (isospin) |
generation 1 |
generation 2 |
generation 3 |
| quarks up-type |
+ 2/3 |
+ 1/2 |
yes |
|
u (up) 3 MeV |
c (charm) 1.2 Gev |
t 175 GeV |
| quarks down-type |
- 1/3 |
- 1/2 |
yes |
|
d (down) 7 MeV |
s (strange) 120 Mev |
b 4.2 GeV |
| leptons neutrinos |
0 |
+ 1/2 |
no |
|
Ve < 3eV |
vT < 18 MeV |
vT 18 MeV |
| leptons charged |
-1 |
- 1/2 |
no |
|
e (electron) 0.511 Mev |
T (muon) 1.78 GeV |
T 1.78 GeV |
Colour neutral quarks (hadrons) can be combined as in following examples:
proton = u + u + d
neutron = u + d = d
Bosons
Bosons are particles which make forces (or do they just transport a force from
one point to another ? I don't really understand this) For example electro-magnetism
travels through materials that photons cant travel through?
| |
|
| electo-magnetism |
photon |
| weak nuclear |
wt
w-1
z0 |
| strong nuclear |
|
| gravitational |
graviton (speculative - not detected yet) |
| |
|
Noether for Quantum Mechanics
See Noethers theorem.
For Particles (fermions) Angular Momentum is quantized. Particle spin and orbital states are always a half integer multiple of h-bar. In other words,
spin = 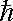 /2, 3*
/2, 3*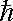 /2 ...
/2 ...
where:
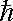 = h/2 PI
= h/2 PI- h = Planck's constant
There is also something strange about the spin in that a rotation of 720 (not 360 degrees) is needed to get back to the original orientation. This can be modeled by quaternion (spinor) where a rotation of 360 degrees inverts all of its x,y,z and w elements.
If we take the Schrödinger's wave function for two particles:
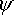 (
(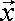 1,
1,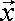 2,t)
2,t)
We can investigate symmetry by exchanging the two particles:
for two bosons: 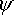 (
(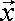 1,
1,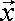 2,t) =
2,t) = 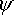 (
(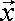 2,
2,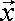 1,t)
1,t)
for two fermions: 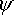 (
(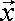 1,
1,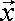 2,t) =-
2,t) =- 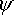 (
(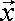 2,
2,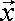 1,t)
1,t)
In other words, if we exchange two identical fermions we invert the wave function. This is equivalent to rotating the system by 180 degrees.
This accounts for the pauli exclusion principle because if two identical particles were superimposed the wave function would be zero.
This site may have errors. Don't use for critical systems.