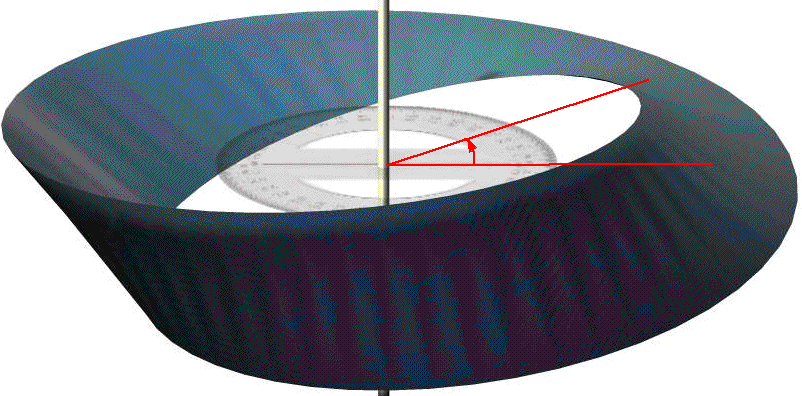
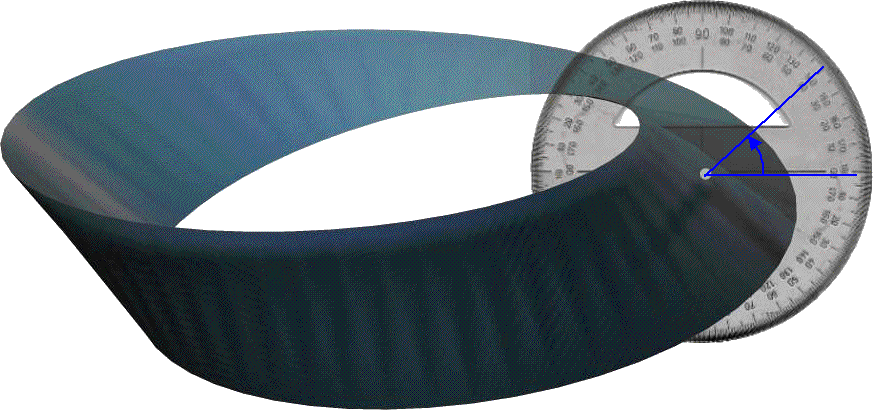
Spinors can represent rotations in 'n' dimensions. It has some interesting properties:
- It can represent conventional rotations (that return to original position after 360° rotation) by using 'sandwich' product: p2 = R p1 R-1.
- It can represent the spin of particles (that return to original position after 720° rotation) by using some other product.
- It can be represented by even subalgebras of Clifford algebras.
- It can be represented by Pauli Matrices
- It is a Lie Group.
History
When reading about subjects as apparently diverse as quantum mechanics, mathematics of rotation, group theory, etc. we often come across the term 'spinor'. Spinors seem to have been discovered independently by physicists (Dirac - ) and mathematicians (Rodrigues also Cartan) so it seems especially difficult to tie down a definition.
While working on quantum theory Dirac found that he needed to take the square root of a vector and he found this produces Spinors. This has to be done in an algebra where products (and hence squares) of vectors make sense (see Clifford algebra)
Conventional Rotations
We can represent rotations in any number of dimensions using 'sandwich' product: p2 = R p1 R-1
where:
- p1 = vector point before rotation
- p2 = vector point after rotation
- R = spinor representing the rotation
- R-1= inverse of spinor representing the rotation
note: each rotation can be represented by 2 spinors (R and -R) which in this case represent the same rotation.
Particle Spin
Because of the warping of time and space at high spin rates (see this page) then a particle does not return to its original state until it does a 720° rotation.
A spinor turns into a negative when it does a 360° rotation.
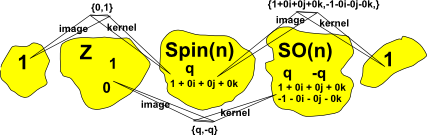
Short Exact Sequence
The spin group appears in the following short exact sequence:
1 -> Z2 -> Spin(n) -> SO(n) -> 1
Definitions:
- A 'short exact sequence' is a sequence of algebraic structures and morphisms between them such that the image of one morphism equals the kernel of the next. Further explanation on this page.
- Z2 is the integers modulo 2 = {0,1}
- Spin(n) is the spin group in n dimensions
- SO(n) is
- -> is a morphism between groups
Note that there is a 1:2 mapping between 1 and Z2 and there is a 2:1 mapping between Spin(n) and SO(n).
In order to try to understand this I have tried to calculate the image and kernel for 3D rotations as represented by a unit quaternion 'q', working this out below I think I have made it fit the definition:
ker (1 -> {0,1}) = 1
im (1 -> {0,1}) = {0,1}
ker ({0,1} -> q ) = {0,1}
im ({0,1} -> q ) = {q,-q}
ker (q -> {q,-q}) = {q,-q}
im (q -> {q,-q}) = {1 + 0 i + 0 j + 0k,-1 - 0 i - 0 j - 0k}
ker ({q,-q} -> 1) = {1 + 0 i + 0 j + 0k,-1 - 0 i - 0 j - 0k}
im ({q,-q} -> 1) = 1
Even Subalgebras of Clifford Algebras
Spinors can be represented mathematically by Even Clifford algebras, I have attempted to prove this (here).
Spinors and Group Theory
In group theory there is a type of group called Spin(n) which has elements known as spinors which is a double cover of the special orthogonal group SO(n).
A Lie group has a set of parameters which continuously map to a topological space (manifold) . The term "double cover" means that this is a 2:1 mapping, i.e. there are 2 different parameter values which map to the same topological position.
There are some restrictions on this, using words like "nontrivial metric signature" which I don't understand, I guess they are there to eliminate some special case?
There are some "accidental isomorphims" at low dimensions. That is some groups, while not being strictly defined as spin groups, coincidentally have the same properties at low dimensions:
- Spin(1) = O(1)
- Spin(2) = U(1)
- Spin(3) = Sp(1) = SU(2)
- Spin(4) = Sp(1) x Sp(1)
- Spin(5) = Sp(2)
- Spin(6) = SU(4)
"There are certain vestiges of these isomorphisms left over for n = 7,8 For higher n these isomorphism disappear entirely."
Assuming that SO(n) is a single cover of the same parameters then it is reasonable that, for a single rotation of SO(n), then Spin(n) will rotate twice for every rotation of SO(n)?
So, although this 2:1 mapping of rotations is not the definition of spinors, it does appear to be a fundamental property which is very closely linked to the definition?
Other definitions:
Group theory: "A linear space which is acted on in a single-sided manner by rotors forms a carrier space for a spin representation of the rotation group. Elements of such a space are generally called spinors"
Geometric Algebra: "even multivectors"
"Relationship between vectors and spinors holds true in 3,4,6 and 10 dimensions (one more than the dimensions of R,C,Q and O which gives the following isomorphisms:
SL(2,R) ≡SO(2,1)
SL(2,C) ≡SO(2,3)
SL(2,Q) ≡SO(2,5)
SL(2,O) ≡SO(2,9)"
where:
- SL(n, F) = The special linear group, consisting of n×n matrices where each element is of type 'F' with determinant =1.
- SO(n,R) = subgroup of E+(n), which consists of direct isometries, i.e., isometries preserving orientation; it contains those which leave the origin fixed. It is the rotation group of the sphere and all objects with spherical symmetry, if the origin is chosen at the center. Every orthogonal matrix has determinant either 1 or −1. The orthogonal n-by-n matrices with determinant 1 form a normal subgroup of O(n,F) known as the special orthogonal group SO(n,F).
If SO(p,q) is defined with two numbers then I think it is the orthogonal group for any symmetric quadratic form Q with matrix signature (p,q). The group of matrices A which preserve Q, is denoted O(p,q). The Lorentz group is O(3,1).
Spinors
I am coming to the view that the important thing about spinors is how they occur in different dimensions. I'll try to explain the reasoning for this:
It seems to me that there are 2 ways that 'algebras' change with different numbers of dimensions:
- related algebras like complex numbers, quaternions and octonions (2,4 and 8 dimensions).
- 'groups' that represent the same thing in different dimensions such as spinors.
The second type are things like the rotation group which represents rotation in any number of dimensions. Spinors represents a double cover of rotation in any number of dimensions. These 'groups' (I'm not sure if I'm using the correct terminology) don't have their own algebra, so if we want to use spinors in a given number of dimensions we have to match it with an algebra from the first type.
which type is su(1),su(2),su(3)... ?
For example if we want to use spinors in 3D we could use either:
- quaternions.
- a subset of 2x2 matrices containing complex numbers (pauli matrices).
These both fully represent (are equivalent to) spinors in 3D.
If I'm correct about all this, then the reason that all the work on this tends to be abstract concepts rather than intuitive ideas, is that our human intuition does not work in 4 or more dimensions (is has some trouble with rotations in 3 dimensions).
So what about 2 dimensions? Does the concept of spinors occur in 2 dimensions? Of course it cant occur in 1 dimension because there are no rotations in 1 dimension.
It does superficially look like quaternions extend the way that complex numbers represent rotations, but I don't think quaternion rotation is an extension the way complex numbers represent rotations, they are completely different. I think it is just a coincidence that they both happen to represent rotations. (if it is valid to use the word 'coincidence' in mathematics). For instance:
- The two dimensions in complex numbers (real and imaginary) can represent coordinates of the objects being rotated. The four dimensions of quaternions have no direct relationship to the 3 dimensions of the objects being rotated.
- In complex numbers rotation is done using complex exponent, in quaternions its done using the 'sandwich' multiplication.
- In complex numbers 'i' represents 90 degree rotation, in quaternions 'i' represents 180 degree rotation.
Spinor Algebra
This section tries to define spinors in terms of geometric algebra.
If we are working purely in 3D then I think the following are isomorphic:
- spinor algebra
- quaternions
- scalar+bivector generated by 3D vectors which square to +ve.
- even grades generated by 3D vectors which square to +ve.
Lounesto's book (see book shop at bottom of this page) talks about Spin(n)
and I think its clear here and elswhere that the idea of spinors is something
that is seen whatever number of dimensions we are working in - and this is
important to the concept otherwise we might as well call them quaternions
instead of spinors.
Do any of the above equivalences apply if we are working with a number of dimensions above 3 or if some of the dimensions are timelike instread of spacelike? If we find that the definition of spinors is something like: 'a double cover of something to do with finite rotation' then it may turn out that the actual grades involved will differ depending on the number of dimensions and what they square to?
One possible definition might be scalar + bivector.
- In 2 dimensions, if the basis vectors are e1 and e2 then the bivector will have 1 dimension e1e2 (there is 1 combination of 2 from 2).
- In 3 dimensions, if the basis vectors are e1, e2 and e3 then the bivector will have 3 dimensions e1e2, e2e3 and e3e1(there are 3 combinations of 2 from 3).
- In 4 dimensions, if the basis vectors are e1, e2 e3 and e4 then the bivector will have 6 dimensions e1e2, e2e3, e3e1, e1e4, e2e4 and e3e4 (there are 6 combinations of 2 from 4).
So if we define a spinor as scalar + bivector, then,
- In 2 dimensions the spinor would have 1+1=2 dimensions which would have an algebra isomorphic to complex numbers.
- In 3 dimensions the spinor would have 1+3=4 dimensions which would have an algebra isomorphic to quaternions.
- In 4 dimensions the spinor would have 1+6=7 dimensions which would have an algebra which is not closed (very messy).
If instead we define a spinor as an even sub algebra of the geometric algebra G+(n,0). Then the 2 and 3 dimensional cases would be the same as the above but for the 4D case there would be an additional psudoscalar term which gives 1+6+1=8 dimensions which would give a closed but not associative algebra.
I don't know if this algebra is isomorpic to octonions? That would be too good to be true. I suspect that if spinors and octonions were isomorphic in 4D we would have heard about it before now.