Maths - Exponential Form of Quaternion

When we looked at complex numbers we saw that they could be represented in what is known as the polar form:

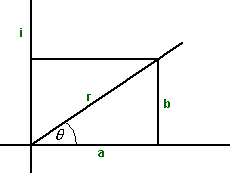
r (cos(θ) + i sin(θ))

in other words replace:

• a = r cos(θ)
• b =r sin(θ)

we can use e^iθ = cos(θ) + i sin(θ) to give the exponential form:

r e^iθ

To combine the result of two rotations, for example rotate by θ1 then rotate by θ2, then we multiply the corresponding complex numbers because:

e^i(θ1+θ2) = e^iθ1 * e^iθ2

Can we do the same with quaternions to represent rotations in 3D?

If we could it would be very useful! For instance, it would be very useful to use:

e^{(a i + b j + c k)} = e^{a i} * e^{b j} * e^{c k}

Unfortunately that doesn't work

e^{(a + b)} = e^a * e^b

is valid when 'a' and 'b' are scalar numbers or complex numbers but it does not work when 'a' and 'b' are quaternions or bivectors (the imaginary part of quaternions). This is because bivectors do not commute for multiplication but they do commute for addition, therefore if we swap a and b in the above equation the left hand side will not change but the right hand will, therefore the equation cannot be true for bivectors.

The valid form of this equation for bivectors is:

e^c = e^a * e^b

where:

c = a + b + a×b + 1/3(a×(a×b)+b×(b×a)) + ...

This is a series known as the Baker-Campbell-Hausdorff formula.

This shows that if when a and b become close to becoming parallel then a×b approaches zero and c approaches a + b so the rotation algebra approaches vector algebra.

An example of this might be living on the surface of the earth which, on the small scale, is like being on a flat surface.

Directed Area