As an example of a permutation group (for an introduction to permutation groups see this page) we will look at a finite subset of the 3D rotation group SO(3), so we will look at all the rotation transforms of a cube that map it to itself. For information about 3D rotations see this page.
We can study cube rotation using the various algebras associated with 3D rotations such as:
- encoding of these rotations in quaternions is shown here.
- encoding of these rotations in matrices is shown here.
- encoding of these rotations in axis-angle is shown here.
- encoding of these rotations in euler angles is shown here.
but the aim on this page is to separate the properties of this rotation in a way that is not dependant on the properties of any specific algebra and instead brings out the higher level symmetries.
Lets take as an example the rotation of a cube in ways that does not change its shape (i.e. multiples of 90° rotations about x, y or z) although we will keep track of the rotations possibly by markings on the faces of the cube. We could have chosen other platonic solids, other then a cube, such as a dodecahedron. These other platonic solids are described on this page.
There are a number of ways to analyise this, one way is to number the vertices and track the effect of each rotation on these vertices.
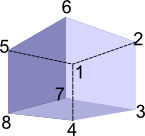
So a 90° rotation about each of the x, y or z axis could be defined as follows (as a cycle decomposition described on this page)
x = rotation about x = (1, 4, 8, 5) (2, 3, 7, 6)
y =rotation about y = (1, 5, 6, 2) (4, 8, 7, 3)
z = rotation about z = (1, 2, 3, 4) (5, 6, 7, 8)
We now need to work out all the permutations of these rotations.
There are 24 made up of 1 identity element, 9 rotations about opposite faces, 8 rotations about opposite vertices and 6 rotations about opposite lines.
| number of rotations | ||
|---|---|---|
| rotate about opposite faces |  |
9 (3 for each pair of faces) |
| rotate about opposite vertices | 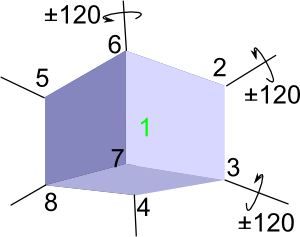 |
8 (2 for each pair of vertices) |
| rotate about opposite lines | 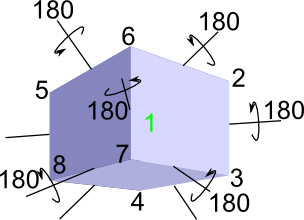 |
6 (one for each pair of lines) |
This gives 9 + 8 + 6 = 23 possible rotations of the cube, plus the identity element (leave it where it is giving 24 possible rotations in total.
There is a quicker way to discover that there are 24 rotations. If we realise that there is a one to one correspondence between rotations and possible orientations of the cube, then all we have to do is count the possible orientations, for instance we could:
- realise that there are 6 faces and so we can place it on each face in turn in 4 possible ways giving 6*4 = 24 possible orientations.
- realise that there are 8 vertices and so we can place it on each vertex in a given position in 3 possible ways giving 8*3 = 24 possible orientations.
Permutation Group of Cube
This has 24 possible rotations, we can generate these by starting with the identity element and the 90° rotations about the x, y and z axis, then by combining these in different sequences we can generate all 24 permutations. In fact, as we shall see below, we only need to start with 2 permutations to generate all possible rotations.
| identity (0°) | about x (90°) | about y (90°) | about z (90°) | |
| permutation | ||||
| cycle notation | (1, 4, 8, 5) (2, 3, 7, 6) | (1, 5, 6, 2) (4, 8, 7, 3) | (1, 2, 3, 4) (5, 6, 7, 8) |
We will denote these permutations by the letters i ,x ,y and z. The composition of x and y (y o x) will be denoted xy:
o |
= |
To be consistent with other literature on this, we need to reverse the order of the functions, that is the right hand function is applied first then the left hand function. So, for example, xy = (y o x).
We can draw up a complete table of the composition operation which defines this example completely. It is a bit of a drudge to work out all these permutations by hand so I have written a program to do this automatically - This is still work in progress - see this page.
Generating rotations from i and x
In order to try out the program with a simple example, I supplied the program with 2 permutations ('i' and 'x') to start it going and it generated two more to complete the group:
| identity (0°) | about x (90°) | about x (180°) | about x (270°) | |
| permutation | ||||
| cycle notation | (1, 4, 8, 5) (2, 3, 7, 6) | (8 1)(7 2)(6 3)(5 4) | (5 8 4 1)(6 7 3 2) |
So from the generators: 'i' and 'x' the program has generated two other permutations 'xx' (apply x twice) and 'xxx' (apply x three times).
The complete multiplication (Cayley) table for this group is then:
| a*b | b.i | b.x | b.xx | b.xxx |
| a.i | i | x | xx | xxx |
| a.x | x | xx | xxx | i |
| a.xx | xx | xxx | i | x |
| a.xxx | xxx | i | x | xx |
Generating rotations from i, x and y
This time I supplied the program with 3 permutations ('i' , 'x' and 'y') to start it going and it generated 21 more to complete the group of 24:
| permutation | ||||
|---|---|---|---|---|
| cycle notation | (1, 4, 8, 5) (2, 3, 7, 6) | (1, 5, 6, 2) (4, 8, 7, 3) | (8 1)(7 2)(6 3)(5 4) | |
| permutation | ||||
| cycle notation | (8 6 1)(4 7 2)(3)(5) | (1)(4 5 2)(8 6 3)(7) | (6 1)(5 2)(8 3)(7 4) | (5 8 4 1)(6 7 3 2) |
| permutation | ||||
| cycle notation | (7 1)(3 2)(6 4)(8 5) | (5 1)(8 2)(7 3)(6 4) | (7 1)(8 2)(4 3)(6 5) | (4 1)(8 2)(5 3)(7 6) |
| permutation | ||||
| cycle notation | (2 1)(5 3)(6 4)(8 7) | (2 6 5 1)(7 8 4 3) | (6 3 1)(2)(5 7 4)(8) | (6 8 1)(7 4 2)(3)(5) |
| permutation | ||||
| cycle notation | (3 1)(4 2)(7 5)(8 6) | (1)(5 4 2)(6 8 3)(7) | (3 8 1)(7 5 2)(4)(6) | (8 3 1)(5 7 2)(4)(6) |
| permutation | ||||
| cycle notation | (3 6 1)(2)(7 5 4)(8) | (2 3 4 1)(6 7 8 5) | (4 3 2 1)(8 7 6 5) | (7 1)(6 2)(5 3)(8 4) |
I don't know if these are the shortest sequences, perhaps I should get the program to check all combinations and see if these are any shorter sequences? At the moment the program allocates the name from the first case of a particular permutation it finds and then subsequent cases are given the original name.
So we don't need to use a third generator 'z' and we already have all 24 possible rotations.

