In order to calculate how a point moves when being rotated in 3D we can use the 'sandwich product' as discussed on this page.
But where does this sandwich product come from? It seems arbitrary, why this function? Is this something that is specific to quaternions or something about rotations that needs this form?
It turns out that the 'sandwich product' is not only used for quaternions. It can be used to represent many other types of transform ... see the pages about geometric algebra, rotors, conformal space and so on.
But the 'sandwich product' is still more general than that, it turns up in group theory and set theory, in this form it is known as a 'conjugacy' (not to be confused with the conjugate of a complex number or quaternion, here a conjugacy is the whole sandwich product).
I think that if we really want to understand where this comes from then we need to delve into this branch of mathematics.
In set theory conjugacy is a way to determine whether two sets (with a multiplication operation - typically a group) are for practical purposes equivalent, that is, isomorphic.
Diagonalizable Matrix
This 'sandwich' product also happens in matrix algebra.
A square n×n matrix A over a field F is called diagonalizable if there exists an invertible matrix P such that P− 1 A P is a diagonal matrix.
P will be the n×n matrix formed with the eigenvectors of A
The resulting diagonal matrix will be a matrix whose diagonal entries are the eigenvalues of A
see wiki page.
Category Theoretic Approach
As discussed on the page here there are two types of algebra associated with transformations (such as rotation) and these algebras must interwork correctly together.
- The first type of algebra defines how a given point is transformed, that is, a given rotation must define where every point, before the rotation, ends up after the rotation.
- The second type of algebra defines how rotations can be combined, that is, we first do 'rotation 1' then we do 'rotation 2' this must be equivalent to some combined rotation, say: 'rotation 3'.
Here we want to do both of these types of algebra using quaternions. To do that a quaternion must be used to represent both a point and a transform, a way to do this is to choose some arbitrary point and then represent all other points as transforms to or from the fixed point (see representable functors on page here). I guess this is a bit like using vectors to represent points in space by using a vector from the origin.
Depending whether we choose a transform 'to' or 'from' will depend on whether a mapping between any two point varies covarient or contravariently with our 'representable' transforms as follows.
Let 'A', 'X' and 'Y' be elements of a class 'C'.
Assume that both 'A' and 'f' are fixed because:
- 'A' is our chosen fixed point.
- 'f' is our chosen mapping from 'X' to 'Y'.
| covarient | contravarient |
|---|---|
So given some fixed 'f' the 'g' depends on 'h' which I have drawn below as an arrow between arrows. |
So given some fixed 'f' the 'h' depends on 'g' which I have drawn below as an arrow between arrows. |
| This arrow goes in the same direction to f, hence it is covarient. | This arrow goes in the opposite direction to f, hence it is contravarient. |
So far in representables we have mapped a element of an object to an element of a homset, but we want to know if this map preserves structure, so here we will see what happens when we map a whole function 'f':
| covarient | contravarient |
|---|---|
 |
 |
From the triangle on the right of the diagram we have: hom(A,Y) = f • hom(A,X) that is post compose with f So f maps to: hom(A,X) -> hom(A,Y) which is: hom(A,X) -> f • hom(A,X) |
From the triangle on the right of the diagram we have: hom(A,X) = hom(A,Y) • f that is pre compose with f So f maps to: hom(A,X) -> hom(A,Y) which is: hom(A,Y) • f -> hom(A,Y) |
So in one case we apply the transform by pre-multipling by 'f' and in the other case we apply the transform by post-multipling by 'f'. However we want the transform to be independent of the arbitrary point 'A', so we end up with a combination of both pre and post-multiplying.
Search For A More Intuitive Explanation
Here we will try to explain this in terms of quaternions:
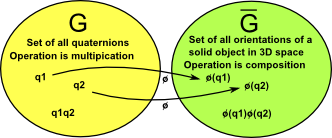
We define some mapping φ from G to G'. We want G and G' to be equivalent to each other, this means that G and G' are isomorphic. This isomorphism means that:
φ(q1*q2) = φ(q1) * φ(q2)
where:
- q1and q2 are quaternions in G
- φ is a one to one mapping from a quaternion to an orientation (lets forget that there is a two to one mapping for now)
So what is this mapping φ? We can use:
φ(v) = q v q-1
so
| φ(q1*q2) = q q1 q2 q-1 = q q1 q-1 q q2 q-1 = φ(q1)*φ(q2) |
(since q-1 q =1) |
So we can see that this sandwich product (conjugacy) has the right properties for an isomorphism (I have investigated what functions form an isomrphism on this page).
What would happen if instead of the sandwich product we tried a simple product:
φ(v) = q v
in this case we would have:
φ(q1*q2) = q q1 q2
but
φ(q1)*φ(q2) = q q1 q q2
which is different so a simple product does not form an isomorphism.
So what about matrix algebra? We can use the mutiplication of a matrix by a vector to rotate a point, why does this work?