So how do we use quaternions to transform one 3D vector into another?
Converting the 3D vector into a quaternion
First we convert the 3D vector into a quaternion, to do this we set the imaginary pars of the quaternion to the x,y and z values of the vector, the real part of the quaternion is set to zero. This quaternion is therefore not normalised like the quaternion representing the rotation.
So we take the vector: (x,y,z)
And represent it by the quaternion: 0 + i x + j y + k z
Now we need to combine this quaternion, representing a point, with a quaternion representing say a rotation?
Multiply q*v
Lets try multiplying them together (as we did for 2D transforms using complex numbers):
q*v = - qx*x - qy*y- qz*z + i (qw*x + qy*z - qz*y) + j (qw*y - qx*z + qz*x) + k (qw*z + qx*y - qy*x)
This does not work, in that it does not produce a pure vector, it has a real term.
So what type of transform would this produce? Rewriting the above equation as a matrix gives:
|
= |
|
|
We can divide this matrix into 3 parts:
|
The real part is minus the dot product of the imaginary part of q and the input vector. | ||||||||||||
|
There is an imaginary component which is the input vector scaled by qw. | ||||||||||||
|
The other imaginary component is a screw symmetric matrix which represents the cross product of qx,qy,qz and the input matrix. This generates a vector which is mutually perpendicular to both v and (qx,qy,qz) this maps v onto a plane perpendicular to v. |
So, if we represent the output quaternion as a scalar and vector (this page), we have
q*v = (imaginary(q)•v, real(q)*v + imaginary(q) × v)
where:
- imaginary(q) = imaginary part of q, in other words (qx,qy,qz) treated as a vector
- real(q) = real part of q which is qw
- • = vector dot product which produces a scalar
- × = vector cross product.
So this does not represent the general rotation that we looking for and we need to do something different.
Example
Lets try a particular example, let q=i, which usually represents a rotation of 180° (reflection in y&z axes), for this
qw=0, qx=1, qy=0, qz=0
which gives the transform:
q*v = - x + j (-z) + k (y)
This seems to have transformed the x axis into the real dimension, the z axis into the y axis and the y axis into the z axis. So it seems to be a sort of rotation by 90°, but outside the 3D space we have created.
Transform of the axes
So in general, how would the axes be transformed by this method?
- if q=1 then q*v=v which gives no change
- if q=i then q*v=i*v which transforms i to -1 and j to k and k to -j which is rotate 90° about x axis and x axis to -real axis.
- if q=j then q*v=j*v which transforms i to -k and j to -1 and k to i which is rotate 90° about y axis and y axis to -real axis.
- if q=k then q*v=k*v which transforms i to -j and j to i and k to -1 which is rotate 90° about z axis and z axis to -real axis.
Multiply v*q'
So lets try a different multiplication this time, instead of 'left multiplying' by q, we will try 'right multiplying' by q'. Where q' is the conjugate of q. This gives the following:
v*q'= x*qx + y*qy+ z*qz + i (x*qw - y*qz + z*qy) + j (x*qz + y*qw - z*qx) + k (- x*qy + y*qx + z*qw)
This also has a real term, but it is equal and opposite to the real term for q*v.
The imaginary terms are exactly the same as the imaginary terms for q*v
Example
Again lets try the same example, let q=i, which usually represents a rotation of 180°.
qw=0, qx=1, qy=0, qz=0
which gives the transform:
v*q'= x + j (- z) + k (y)
Transform of the axes
So in general, how would the axes be transformed by this method?
- if q=1 then q*v=v which gives no change
- if q=i then v*q'=v*(-i) which transforms i to +1 and j to k and k to -j which is rotate 90° about x axis and x axis to +real axis.
- if q=j then v*q'=v*(-j) which transforms i to -k and j to +1 and k to i which is rotate 90° about y axis and y axis to +real axis.
- if q=k then v*q'=v*(-k) which transforms i to -j and j to i and k to +1 which is rotate 90° about z axis and z axis to +real axis.
So both of these produce give half the required rotation, but one gives a positive real part and the other gives a negative real part. So can we combine them to give the full rotation with no real part?
Multiply q * P1 * q'
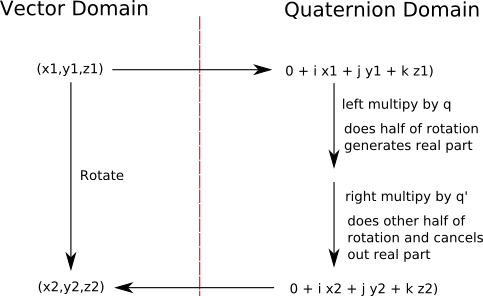
For Rotation: P2=q * P1 * q'
Which gives:
P2.x = x*(qx*qx+qw*qw-qy*qy- qz*qz) + y*(2*qx*qy- 2*qw*qz) + z*(2*qx*qz+ 2*qw*qy)
P2.y = x*(2*qw*qz + 2*qx*qy) + y*(qw*qw - qx*qx+ qy*qy - qz*qz)+ z*(-2*qw*qx+
2*qy*qz)
P2.z = x*(-2*qw*qy+ 2*qx*qz) + y*(2*qw*qx+ 2*qy*qz)+ z*(qw*qw - qx*qx- qy*qy+
qz*qz)
Where:
- P2 = output vector
- P1 = input vector
- q = quaternion representing rotation
Which represents the required rotation
Example
Again lets try the same example, let q=i.
qw=0, qx=1, qy=0, qz=0
Which gives:
P2.x = x
P2.y = -y
P2.z = -z
A rotation of 180° as required.
Transform of the axes
So in general, how would the axes be transformed by this method?
If q is a different axis from v then the axis will be inverted:
j*i*(-j) = -i
If q is on the same axis from v or q is real then the axis will not be changed:
i*i*(-i) = i
- if q=1 then q*v*q'=v which gives no change
- if q=i then q*v*q'=i*v*(-i) which inverts the j and k axes
- if q=j then q*v*q'=j*v*(-j) which inverts the i and k axes
- if q=k then q*v*q'=k*v*(-k) which inverts the i and j axes
Inverting an odd number of axes produces a reflection, inverting an even number of axes produces a rotation, so this produces a rotation.
Reflection

Reflection is the same as rotation except when we right multiply we use q instead of q'. This gives:
v*q= -x*qx - y*qy- z*qz + i (x*qw + y*qz - z*qy) + j (- x*qz + y*qw + z*qx) + k (x*qy - y*qx + z*qw)
Again lets try the same example, let q=i.
qw=0, qx=1, qy=0, qz=0
Which gives:
v*q= -x + j (z) + k (- y)
This changes the real part in the same way as left multiplying. However the imaginary part is rotated in the opposite direction to left multiplying.
Transform of the axes
So in general, how would the axes be transformed by this method?
If q is a different axis from v or q is real then the axis will not be changed:
j*i*j = i
If q is on the same axis from v then the axis will be inverted:
i*i*i = -i
- if q=1 then q*v*q'=v which gives no change
- if q=i then q*v*q'=i*v*i which inverts the i axis.
- if q=j then q*v*q'=j*v*j which inverts the j axis.
- if q=k then q*v*q'=k*v*k which inverts the k axis.
Inverting an odd number of axes produces a reflection, inverting an even number of axes produces a rotation, so this produces a reflection.
q * P1 * q conclusions.
I'm not sure how to interpret this? perhaps when we combine the multiplications using:
P2=q * P1 * q
the rotations are cancelled out? But how does the real part disappear?
Summary
This page gives a justification of the equation for translating 3D vectors using quaternions.
P2=q * P1 * q'
It is not a rigorous proof but I think it gives a good indication of why we do the translating in this way.
There is a more brute force demonstration of this equation here but it does not really give any insight as to where the equation comes from.
I would welcome ideas for a more rigorous version of this page. I think there is a more general result from Clifford Algebra, which is that:
P2=m * P1 * reverse(m)
always preserves the order of the multivector for an even Clifford algebra.
i.e. If P1 is a pure vector then P2 will be pure vector.