Maths - Sets

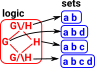
A set is a collection of things, which are called the elements of the set.

"an abstract set X has elements each of which has no internal structure whatsoever" - Lawvere.

In mathematics 'set' is a fundamental concept but there are different approaches that can be taken to it:

• There are various formulations of set theory. In, say the ZF formulation, everything is a set.
• Often we may look at set as a sort of minimal structure onto which we can add extra structure.
• In computing a set may be seen as a collection, like a list, where there are no duplicates and order is not important.
• There is a correspondence between set theory and second order logic.

Here we mostly treat set as a minimal structure, with the concept of set membership and subsets, onto which we can add other structures.

Concepts

Sets can be specified in various ways:

Principle of Comprehension

If φ(x) is a property of object x then there exists a set whose elements have that property.

Equality

In Set Theory More on page here.		Two sets are equal if they contain the same elements (Principle of Extensionality). If the set has structure then that would also have to be equal in some way.
In Category Theory More on page here.		Often when comparing types we need some loser way of considering that two types are essentially the same. Isomorphism is frequently the most appropriate type of equality. This is defined using a category theory way, that is, by external morphisms.
In Type Theory More on page here.	vec(x)=vec(x+0)	In M-L type theory the Identity type is often used. If things are equal in this way they can be interchanged when used in computer programs.
In Type Theory More on page here.		In Homotopy Type Theory (HoTT) there is a different way to get isomorphism from equality. That is to allow types to be equal in many ways.

Set Theory In, say the ZF formulation of set theory, everything is a set.The elements of a set are themselves sets and their elements are sets. Its sets all the way down until we get to an empty set. Also an element cannot occur more than once in a set so a given set can't contain more than one empty set. An element can occur in more than one set but loops would allow paradoxes. This is a difference between set theory and type theory, the page here discusses the relationship between set theory and type theory.

Set + Structure

In its purest form the only information contained in a set is the number of elements it contains. All other information, such as labeling the elements, can be added using functions between sets.

A total function maps every element in the domain to an element in the codomain. Although not every element in the codomain may necessarily be mapped too. So, in this way functions between sets are not necessarily symmetrical.

From this mathematical structure is genererated.

Bijective functions are invertible. See: Isomorphism in Category Theory
Surjective functions are not invertible in that we can't reverse the function and get back to where we started, for instance if we have a surjective mapping from set to set we can't get back to the same set, however we can go back to a 'set of sets'. This gives rise to interesting structure, see: Fibre in Topology Fibre in Category Theory Dependant Type in Type Theory
Injective functions gives a subobject structure. If we have an injective mapping from set to set we can't get back to the same set, however we can have a mapping from set to Bool which tells us which element are in the subset, this is known as a characteristic function in sets or 'subobject classifier' more generally in category theory. This subobject structure is interesting see: Subobject in Topos Theory Pullback in Category Theory Subobject classifier

This page explains bijection, injection and surjection.

Inverse Functions

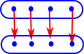
In general a function is not invertible, in that if we reverse all the arrows we don't necessarily get back to where we started. Bijective functions are invertible but reversing the arrows in injective and surjective functions gives something that is not a function.

Lets look an example where we try to invert an surjective function.
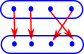
If we try to invert this example some of the elements in the domain go to multiple elements in the codomain so this is not a total function. In category theory we can have arrows which are more general than functions so there would be some categories where this is valid but not the category of set.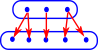
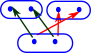
So what is the closest we could get to this using ordinary functions?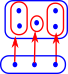
Lets look an example where we try to invert an injective function.
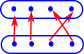
If we try to invert this example there is nowhere for the first two elements to go so this is not a total function. Again, in category theory we can have arrows which are more general than functions so there would be some categories where this is valid but not the category of set.
So what is the closest we could get to this using ordinary functions?

Proofs about Sets

A key part of mathematics is proofs.

In order to prove things about sets we need a logic layer underpinning it.

Proofs in Isabelle

Isabelle is a program known as a proof assistant. More about this program on this page.

In Isabelle sets are typed. All elements have the same type (say τ) and the set itself has the type τ set (the order of type constructors is reversed compared to many languages). A type variable a is written: 'a so a set of these is written: 'a set.

Isabelle Notation	Meaning
a ∈ A	A is a member of B
a ∉ A	A is not a member of B
{}	empty set
UNIV	universal set
{a,b,c}	a finite set consisting of elements a,b and c
{x. P}	comprehension set of all elements that satisfy predicate P
{p*q | p q. pprime /\ qprime}	more complicated comprehension in this case all numbers which are the products of two primes. Could also be represented by: {x.p q. z = p*q /\ pprime /\ qprime}
AB	A is a subset of B

Set Membership

The Isabelle code (from this site) starts with two concepts:

• member () Membership is the key concept of sets. In Isabelle it is a binary operator which takes a element and a set and returns true if the element is a member of the set.
• Collect infers the members of a set from a predicate, this is known as set comprehension.

axiomatization Collect :: "('a => bool) => 'a set" -- "comprehension"
  and member :: "'a => 'a set => bool" -- "membership"
where
  mem_Collect_eq [iff, code_unfold]: "member a (Collect P) = P a"
  and Collect_mem_eq [simp]: "Collect (λx. member x A) = A"
  
notation (HTML output)
  member      ("op ∈") and
  member      ("(_/ ∈ _)" [51, 51] 50) and
  not_member  ("op ∉") and
  not_member  ("(_/ ∉ _)" [51, 51] 50)

The axioms show Collect and member as being some sort of inverse. that is, Collect allows us to compose a set and member allows us to decompose it.

In category theory a function a subobject classifier has the type: 'a set => bool.

Set comprehension is a construction that allows us to define a set by stating the properties of its members.

Mappings

Mappings, functions between sets are discussed on page here.

Subset

AB means A is a subset of B

AB iffxA : xB

Subsets and Logic

There is a relationship between subsets and logic.

This can give rise to different set theories, for instance, constructive or intuitionistic logic gives rise to constructive set theory.

Intersection, Union and Venn Diagrams

Intersection The intersection of two sets is another set which contains the elements in both the original sets.
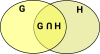Union The intersection of two sets is another set which contains all the elements from original sets, if an element is in both the original sets then it is only included once, not twice.
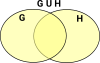Complement This is everything not in the set. This has to be defined in terms of the universe under discussion.

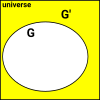Cartesian Product

The Cartesian product of two sets is a set of pairs representing every combination of the two sets. This is a very general product that we can define regardless of whether multiplication is a valid operation for the elements of the sets being multiplied. So this type of product 'generates' a higher dimensional quantity.

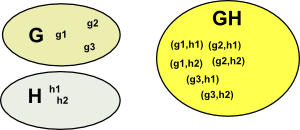So what happens when we multiply two of these two dimensional quantities?

(g1,h1)(g2,h2) = ?

Perhaps it might generate a 4 dimensional quantity:

(g1,h1)(g2,h2) = (g1,h1,g2,h2)

Or we might be able to define a multiplication which would make this equivalent to complex number multiplication:

(g1,h1)(g2,h2) = (g1g2 - h1h2 , g1h2 + g2h1)

Or we may require a different definition,as an example, lets take the dihedral group D3, that we looked at on this page. We might represent any transform as a pair like:

(ma,ra)

Consisting of one reflection and one rotation, we can represent any element of this group by such a pair.

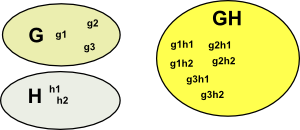
Lets take another example, imagine that we have a group G and a subgroup H with elements g1,g2… and h1,h2…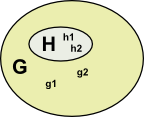

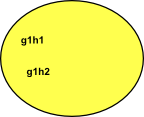
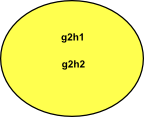
In this case we can now define multiplication as g1 H * g2 H = g1 g2 H

g1 H	g2 H	g1 g2 H
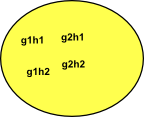left coset g1 of H	left coset g2 of H	left coset g1,g2 of H

Product

If multiplying individual elements of the first set by elements of the second set is valid, then the product no longer needs to be represented by pairs, in this case the product contains the product of every combination of the two sets. If we are combining two groups then we may be able to use an external or internal product as described on this page.

Equivalence Relation

Generalisation of equality to set theory.

If two sets are exactly equal, this may not be all that interesting from a mathematical point of view. It is often more interesting when two sets are not identical but preserve some form of structure when mapping between them.

	type	category notation
tighter	Equality
	Isomorphism	1 = GF FG = 1
	Equivalence	1GF FG1
looser	Adjunctions	1 => GF FG => 1

Equivalence:

Set Notation	Alternative Notation	Property
(a,a)R for all aS	aa	Reflective
(a,b)R implies (b,a)R	ab implies ba	Symmetric
(a,b)R and (b,c)R implies (a,c)R	ab and bc implies ac	Transitive

Sequence in a set

A function from N (the set of positive integers) to the set.

In other words each element of the set is assigned a number.

Notation:

{a_n}_n=1^∞

Indexing sets

An index set is a set used to label the elements of another set using a surjective function.

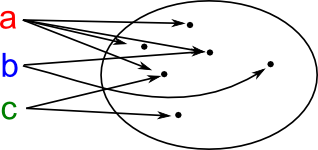
An alternative approach is to attach a name to each element of a collection of sets.

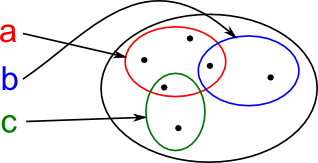
Notation:

{a_α}_α∈A

Related Topics

• Open and closed sets.
• Proofs for sets using Isabelle.

Next

Mappings, functions between sets are discussed on page here.

EuclideanSpace

home

Related Pages

• The page here discusses the relationship between set theory and type theory.
• Mappings, functions between sets are discussed on page here.
• Sets, from the point of view of category theory, are discussed on page here.
• An extension to sets is the Setoid structure.

Venn Diagrams

Some of us, of a certain age, can remember something called 'new maths' introduced at school. This was an idea to introduce set theory at an early stage (I hope they still do it). An important part of this was Venn diagrams, they give a very intuitive way to look at sets and their intersections and unions. For me an important part of this is the way it demonstrates a deep and beautiful link between sets (union, intersection), logic (and, or) and topology.

Sets, Logic and Topology

There is a problem with Venn diagrams, they do not work so well when we increase the number of sets. Its alright with 3 sets, we can draw 3 circles showing all possible intersections, but its more difficult with 4 or more sets.

To have a diagram that scales up to many sets it seems to be necessary to separate the sets from the logic. This diagram is less intuitive and compact than Venn diagrams but it is still very powerful. It must obey certain axioms so that the sets are consistent with the logic part. For more information see the page about sheaves.

Set Symbols

1:1 Correspondence Definition

Function Definition

Morphism (homomorphism) Definition

Representation Definition

Category Theory

Sets for Mathematics - This is a book about sets from category theory point of view.

Example - Database

Here we look at types of functions between sets in terms of a relational database. More information about databases on page here.

I think this gives a slightly different way to think about functions that