Maths - Conversion Matrix to Quaternion

Matrix to Quaternion Calculator.

Equations

For a pure rotation, that is where:

the matrix is orthogonal
the matrix is special orthogonal which gives additional condition: det(matrix)= +1

Then the matrix can be converted to a quaternion using this basic form:

qw= √(1 + m00 + m11 + m22) /2
qx = (m21 - m12)/( 4 *qw)
qy = (m02 - m20)/( 4 *qw)
qz = (m10 - m01)/( 4 *qw)

But this is only accurate under certain conditions and to get an algorithm that is accurate under all circumstances we need to check the trace as below:

Java Code

Simple Code

public final void set(Matrix4f m1) {
	w = Math.sqrt(1.0 + m1.m00 + m1.m11 + m1.m22) / 2.0;
	double w4 = (4.0 * w);
	x = (m1.m21 - m1.m12) / w4 ;
	y = (m1.m02 - m1.m20) / w4 ;
	z = (m1.m10 - m1.m01) / w4 ;
}

The above should work assuming that the function inside the square root is positive, that is,

1 + Tr < 0

where Tr = the trace which is the sum of the leading diagonal terms.

For instance the following matrix represents a 180° rotation about the y axis:

-1	0	0
0	1	0
0	0	-1

In this case the above algorithm wont work because 1 + m00 + m11 + m22 = 0 which gives w=0 and so will cause division by zero.

Another example is a rotation of heading= 180° and attitude = 90°.

0	1	0
1	0	0
0	0	-1

Even if the value of qw is very small it may produce big numerical errors when dividing. So it is better to use the following:

1) Calculate the trace(the sum of the diagonal elements) of the matrix T from the equation:

T = 4 - 4*qx² - 4*qy² - 4*qz²
= 4( 1 -qx² - qy² - qz² )
= m00 + m11 + m22 + 1

If the trace of the matrix is greater than zero, then the result is:

      S = 0.5 / sqrt(T)
      W = 0.25 / S
      X = ( m21 - m12 ) * S
      Y = ( m02 - m20 ) * S
      Z = ( m10 - m01 ) * S

If the trace of the matrix is less than or equal to zero then identify which major diagonal element has the greatest value.

Code

float tr = m00 + m11 + m22

if (tr > 0) { 
  float S = sqrt(tr+1.0) * 2; // S=4*qw 
  qw = 0.25 * S;
  qx = (m21 - m12) / S;
  qy = (m02 - m20) / S; 
  qz = (m10 - m01) / S; 
} else if ((m00 > m11)&(m00 > m22)) { 
  float S = sqrt(1.0 + m00 - m11 - m22) * 2; // S=4*qx 
  qw = (m21 - m12) / S;
  qx = 0.25 * S;
  qy = (m01 + m10) / S; 
  qz = (m02 + m20) / S; 
} else if (m11 > m22) { 
  float S = sqrt(1.0 + m11 - m00 - m22) * 2; // S=4*qy
  qw = (m02 - m20) / S;
  qx = (m01 + m10) / S; 
  qy = 0.25 * S;
  qz = (m12 + m21) / S; 
} else { 
  float S = sqrt(1.0 + m22 - m00 - m11) * 2; // S=4*qz
  qw = (m10 - m01) / S;
  qx = (m02 + m20) / S;
  qy = (m12 + m21) / S;
  qz = 0.25 * S;
}

We need to be sure this code is resilient to:

Avoid division by zero - We need to be sure that S is never zero even with possible floating point errors or de-orthogonalised matrix input.
Avoid square root of a negative number. - We need to be sure that the tr value chosen is never negative even with possible floating point errors or de-orthogonalised matrix input.
Accuracy of dividing by (and square rooting) a very small number.
with floating point numbers, dividing small numbers by small numbers should be reasonably accurate but at the extreme it would loose accuracy.
Resilient to a de-orthogonalised matrix

For a discussion of the stability of this code see this forum discussion that I had with Ethan.

Issues

(1) This page assumes that the input matrix represents a pure rotation otherwise the resulting quaternion will not be valid. This implies that the matrix must be special orthogonal, that is both:

the matrix is orthogonal
In addition the matrix is special orthogonal (pure rotation without reflection component)

If these conditions are satisfied then the resulting quaternion should be normalised (unit length).

(2) Both matrices and quaternions avoid the singularities and discontinuities involved with rotation in 3 dimensions by adding extra dimensions. This has the effect that different values could represent the same rotation, for example quaternion q and -q represent the same rotation. It is therefore possible that, if we are converting a rotation sequence, our output may jump between these equivalent forms. This could cause problems where subsequent operations such as differentiation is done on this data. So programmers need to be aware of this issue.

For a more detailed discussuion of these issues see this forum discussion that I had with Tim.

C++ Code (kindly sent to me by Angel)

There is also code from minorlogic at the end of this page. This includes code for both normalised and unnormalised quaternions.

inline void CalculateRotation( Quaternion& q ) const {
  float trace = a[0][0] + a[1][1] + a[2][2]; // I removed + 1.0f; see discussion with Ethan
  if( trace > 0 ) {// I changed M_EPSILON to 0
    float s = 0.5f / sqrtf(trace+ 1.0f);
    q.w = 0.25f / s;
    q.x = ( a[2][1] - a[1][2] ) * s;
    q.y = ( a[0][2] - a[2][0] ) * s;
    q.z = ( a[1][0] - a[0][1] ) * s;
  } else {
    if ( a[0][0] > a[1][1] && a[0][0] > a[2][2] ) {
      float s = 2.0f * sqrtf( 1.0f + a[0][0] - a[1][1] - a[2][2]);
      q.w = (a[2][1] - a[1][2] ) / s;
      q.x = 0.25f * s;
      q.y = (a[0][1] + a[1][0] ) / s;
      q.z = (a[0][2] + a[2][0] ) / s;
    } else if (a[1][1] > a[2][2]) {
      float s = 2.0f * sqrtf( 1.0f + a[1][1] - a[0][0] - a[2][2]);
      q.w = (a[0][2] - a[2][0] ) / s;
      q.x = (a[0][1] + a[1][0] ) / s;
      q.y = 0.25f * s;
      q.z = (a[1][2] + a[2][1] ) / s;
    } else {
      float s = 2.0f * sqrtf( 1.0f + a[2][2] - a[0][0] - a[1][1] );
      q.w = (a[1][0] - a[0][1] ) / s;
      q.x = (a[0][2] + a[2][0] ) / s;
      q.y = (a[1][2] + a[2][1] ) / s;
      q.z = 0.25f * s;
    }
  }
}

Alternative Method

Christian has suggested an alternative algorithm and he makes a convincing argument that this is more efficient here.

There is a potential issue with the use of 'copysign' as described here.

quaternion.w = sqrt( max( 0, 1 + m00 + m11 + m22 ) ) / 2;
quaternion.x = sqrt( max( 0, 1 + m00 - m11 - m22 ) ) / 2;
quaternion.y = sqrt( max( 0, 1 - m00 + m11 - m22 ) ) / 2;
quaternion.z = sqrt( max( 0, 1 - m00 - m11 + m22 ) ) / 2;
Q.x = _copysign( Q.x, m21 - m12 )
Q.y = _copysign( Q.y, m02 - m20 )
Q.z = _copysign( Q.z, m10 - m01 )

The max( 0, ... ) is just a safeguard against rounding error.
copysign takes the sign from the second term and sets the sign of the first without altering the magnitude, I don't know of a java equivalent.

Scaling

Since it is possible for both matrices and quaternions to represent scaling in addition to rotation, then it would be possible to include this in the convertion. In most cases this is not necessary, as we only want to represent rotations, but if you do need to include a scale factor then you might want to try this method suggested by Christian.

Of course, this will mean that the matrix is no longer orthogonal and that the quaternion is no longer normalised.

We first calculate absQ2 which is the cube root of the volume spanned by the matrix axes.

absQ2 = det( matrix )^(1/3)

quaternion.w = sqrt( max( 0, absQ2 + m00 + m11 + m22 ) ) / 2;

...etc

Rounding Errors

When comparing different methods of doing this conversion I think we should consider sensitivity to rounding errors. In other words, the matrix contains redundant information so, althrough a matrix may initially be orthogonal, if we then do some rotation operations rounding errors may de-orthogonalise the matrix, if this happens which method is most likely to cancel out the errors?

I don't know how best to tackle this? say, for instance, rounding errors introduce an error 'delta e' to one element of the matrix, but we don't know which element has the error. Which method is most likely to cancel out this error? Which method is most likely to produce a normalised quaternion?

Derivation of Equations

Quaternion multiplication and orthogonal matrix multiplication can both be used to represent rotation. If a quaternion is represented by qw + i qx + j qy + k qz , then the equivalent matrix, to represent the same rotation, is:

1 - 2qy² - 2qz²	2qxqy - 2qzqw	2qxqz + 2qyqw
2qxqy + 2qzqw	1 - 2qx² - 2qz²	2qyqz - 2qxqw
2qxqz - 2qyqw	2qyqz + 2qxqw	1 - 2qx² - 2qy²

This assumes that the quaternion is normalised (qw² + qx² + qy² + qz² =1) and that the matrix is orthogonal.

This page discusses the equivalence of quaternion multiplication and orthogonal matrix multiplication.

So this gives the following equations:

m00 = 1 - 2*qy² - 2*qz²
m01 = 2*qx*qy - 2*qz*qw
m02 = 2*qx*qz + 2*qy*qw
m10 = 2*qx*qy + 2*qz*qw
m11 = 1 - 2*qx² - 2*qz²
m12 = 2*qy*qz - 2*qx*qw
m20 = 2*qx*qz - 2*qy*qw
m21 = 2*qy*qz + 2*qx*qw
m22 = 1 - 2*qx² - 2*qy²

This contains more information than we need, so we need to choose a method which is less sensitive to matrix not being orthogonal.

If the quaternion is normalised: qx² + qy² + qz²+ qw² = 1

so,

qw² = 1 - qx² - qy² - qz²

multiply both sides by 4 gives,

4 * qw² = 4 - 4*qx² - 4*qy² - 4*qz²

4 * qw² = 1 + 1 - 2*qy² - 2*qz² + 1 - 2*qx² - 2*qz² + 1 - 2*qx² - 2*qy²

4 * qw² = 1 + m00 + m11 + m22

so qw= ±½√(1 + m00 + m11 + m22)

the sum of the diagonal elements is known as the trace (Tr), this gives,

qw= sqrt (1 + Tr) /2

this method can only be used if we are taking the square root of a positive number ie,

1 + Tr <= 0

Is this always the case for orthogonal matrices ???

So we have an equation for qw, to get the other values we can use:

m21 - m12 = 2*qy*qz - 2*qx*qw - 2*qy*qz - 2*qx*qw

m21 - m12 = 4 *qx*qw

therefore:

qx = (m21 - m12)/( 4 *qw)

now calculate qy

m02 - m20 = 2*qx*qz + 2*qy*qw - 2*qx*qz + 2*qy*qw

m02 - m20 = 4*qy*qw

therefore:

qy = (m02 - m20)/( 4 *qw)

now calculate qz,

m10 - m01 = 2*qx*qy + 2*qz*qw - 2*qx*qy + 2*qz*qw

m10 - m01 = 4*qz*qw

therefore:

qz = (m10 - m01)/( 4 *qw)

so summarising the results:

qw= ±½√(1 + m00 + m11 + m22)
qx = (m21 - m12)/( 4 *qw)
qy = (m02 - m20)/( 4 *qw)
qz = (m10 - m01)/( 4 *qw)

Different Methods

There are 4 related methods to calculate the conversion. This gives us alternatives to calculate the result when the simple method above would require us to calculate the square root of a negative number. We can calculate either of the quaternion terms (qw, qx, qy or qz) from the leading diagonal terms of the matrix and then calculate the other terms from the non-diagonal terms:

m00=1 - 2qy² - 2qz²	m01=2qxqy - 2qzqw	m02=2qxqz + 2qyqw
m10=2qxqy + 2qzqw	m11=1 - 2qx² - 2qz²	m12=2qyqz - 2qxqw
m20=2qxqz - 2qyqw	m21=2qyqz + 2qxqw	m22=1 - 2qx² - 2qy²

By adding and subtracting these terms we can separate out the quaternion terms.

From the diagonal terms:

qw=±½√(1 + m00 + m11 + m22)
qx=±½√(1 + m00 - m11 - m22)
qy=±½√(1 + m11 - m00 - m22)
qz=±½√(1 + m22 - m00 - m11)

From the non diagonal terms (subtracting terms):

qx*qw = ¼(m21-m12)
qy*qw = ¼(m02-m20)
qz*qw = ¼(m10-m01)

From the non diagonal terms (adding terms):

qy*qz = ¼(m21+m12)
qx*qz = ¼(m02+m20)
qx*qy = ¼(m10+m01)

combining these diagonal and non-diagonal results we get:

Coordinate Systems

Spinor

Standards

Bilinear and Quadratic Forms

A quadratic form is an expression in a number of variables where each term is of degree two.

Every quadratic form can be represented by a symmetric matrix, to generate the quadratic form we pre-multiply the matrix by a single row vector containing the variables and post-multiply the matrix by a single column vector also containing the variables.

1	3
3	1

=x² + 6xy + y²

More about bilinear form on this page and quadratic form on this page.

method 1 (qw from diagonal)	method 2 (qx from diagonal)	method 3 (qy from diagonal)	method 4 (qz from diagonal)
qw=±½√(1 + m00 + m11 + m22)	qxqw = ¼(m21-m12) gives: qw = (m21-m12)/(4qx)	qyqw = ¼(m02-m20) gives: qw = (m02-m20)/(4qy)	qzqw = ¼(m10-m01) gives: qw = (m10-m01)/(4qz)
m21 - m12 = 2qyqz - 2qxqw - 2qyqz - 2qxqw m21 - m12 = 4 qxqw therefore: qx = (m21 - m12)/( 4 *qw)	1 + m00 - m11 - m22 = 1 + 1 - 2qy² - 2qz² - 1 + 2qx² + 2qz² - 1 + 2qx² + 2qy² = 4*qx² therefore: qx=±½√(1 + m00 - m11 - m22)	qxqy = ¼(m10+m01) gives: qx = (m10+m01)/(4qy)	qxqz = ¼(m02+m20) gives: qx = (m02+m20)/(4qz)
m02 - m20 = 2qxqz + 2qyqw - 2qxqz + 2qyqw m02 - m20 = 4qyqw therefore: qy = (m02 - m20)/( 4 *qw)	qxqy = ¼(m10+m01) gives: qy = (m10+m01)/(4qx)	1 + m11 - m00 - m22 = 1 + 1 - 2qx² - 2qz² - 1 + 2qy² + 2qz² - 1 + 2qx² + 2qy² = 4*qy² therefore: qy=±½√(1 + m11 - m00 - m22)	qyqz = ¼(m21+m12) gives: qy = (m21+m12)/(4qz)
m10 - m01 = 2qxqy + 2qzqw - 2qxqy + 2qzqw m10 - m01 = 4qzqw therefore: qz = (m10 - m01)/( 4 *qw)	qxqz = ¼(m02+m20) gives: qz = (m02+m20)/(4qx)	qyqz = ¼(m21+m12) gives: qz = (m21+m12)/(4qy)	1 + m22 - m00 - m11 = 1 +1 - 2qx² - 2qy² - 1 + 2qy² + 2qz² - 1 + 2qx² + 2qz² = 4*qz² therefore: qz=±½√(1 + m22 - m00 - m11)

So, in theory, we can calculate the quaternion from just the diagonal terms. This would require us to calculate 4 square roots, there is a problem with this, the result of a square root may be either positive or negative and therefore we can't determine the signs of the terms. It is therefore better to calculate one quaternion term from the diagonal and the remaining terms from the non-diagonal. We still have to choose the sign of this first term, we can choose either positive or negative because there are two possible quaternions that can represent any given 3D rotation, what matters is the relative signs of the terms.

Another issue is the speed of the calculation, the square root function has always been taken to be slow, this may be less so on modern computers. I must admit, I have not tested it, but even so I think its best to minimise the number of square roots.

Perhaps the most important issue is the accuracy of the result, if the value derived from the diagonal is small, then any errors in this value will be multiplied up when we calculate the other values. Therefore we may get the most accurate result if we choose the column in the table above which not only avoids the square root of a negative number but also gives the largest diagonal term for the particular rotation that we are calculating.

Rotation about a point other than origin

Quaternions and 3×3 matrices alone can only represent rotations about the origin. But if we include a 3D vector with the quaternion we can use this to represent the point about which we are rotating. Also if we use a 4×4 matrix then this can hold a translation (as explained here) and therefore can specify a rotation about a point.

The following code generates a 3D vector (representing the centre of rotation) from the 4x4 matrix. The theory is given here.

= 1/det[m] *

(m11 - 1)m22 - m12m21	m02m21 - m01(m22 - 1)	m01m12 - m02(m11 - 1)
m12m20 - m10(m22 - 1)	m00(m22 - 1) - m02m20	m02m10 - (m00 - 1)m12
m10m21 - (m11 - 1)m20	m01m20 - (m00 - 1)m21	m00(m11 - 1) - m01m10

m03

m13

m23

Example

we take the 90 degree rotation from this:

to this:

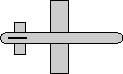As shown here the matrix for this rotation is:

[R] =

1	0	0
0	0	-1
0	1	0

So using the above result:

qw= sqrt (1 + m00 + m11 + m22) /2 = sqrt (2)/2 = 1.4142/2 = 0.7071
qx = (m21 - m12)/( 4 *qw) = 2/(4 * 0.7071) = 1/ 1.4142 = 0.7071
qy = (m02 - m20)/( 4 *qw) = 0
qz = (m10 - m01)/( 4 *qw) = 0

This gives the quaternion 0.7071 + i 0.7071

As you can see here, this gives the result that we are looking for.

Angle Calculator and Further examples

I have put a java applet here which allows the values to be entered and the converted values shown along with a graphical representation of the orientation.

Also further examples in 90 degree steps here

Here is a simple javascript calculator, input matrix values then press calculate button:

EuclideanSpace

home

Prerequisites

Definition of terms:

Matrix vs. Quaternion

If you need to work with rotations in your program is it best to use maricies or quaternions?

Some advantages of quaternions are:

Each quaternion only requires 4 scalars whereas a matrix requires 9 scalars.
It is easier to interpolate between quaternions using SLERP as explained on this page.
Quaternions are easier to normalise than matrices (to cancel out a build up of small rounding errors).

Some advantages of matrices are:

Transforming a point seems simpler by multiplying a vector by a matrix rather than the sandwich form required for quaternions.
People often find matrices easier to understand than quaternions.
There are more ready built matrix libraries than quaternion libraries.

Isometries and Physics

If we want to model isometries, such as the movement of solid bodies, combining rotation and translation, in one single operation, we need to expand the above algebras to model translations as well as rotations.

To model isometries we could either:

Expand matrices to 4x4 as described on this page.
Expand quaternions to dual quaternions as described on this page.

To investigate these issues further see This page.

m00=1 - 2qy² - 2qz²	m01=2qxqy - 2qzqw	m02=2qxqz + 2qyqw
m10=2qxqy + 2qzqw	m11=1 - 2qx² - 2qz²	m12=2qyqz - 2qxqw
m20=2qxqz - 2qyqw	m21=2qyqz + 2qxqw	m22=1 - 2qx² - 2qy²

method 1 (qw from diagonal)	method 2 (qx from diagonal)	method 3 (qy from diagonal)	method 4 (qz from diagonal)
qw=±½√(1 + m00 + m11 + m22)	qxqw = ¼(m21-m12) gives: qw = (m21-m12)/(4qx)	qyqw = ¼(m02-m20) gives: qw = (m02-m20)/(4qy)	qzqw = ¼(m10-m01) gives: qw = (m10-m01)/(4qz)
m21 - m12 = 2qyqz - 2qxqw - 2qyqz - 2qxqw m21 - m12 = 4 qxqw therefore: qx = (m21 - m12)/( 4 *qw)	1 + m00 - m11 - m22 = 1 + 1 - 2qy² - 2qz² - 1 + 2qx² + 2qz² - 1 + 2qx² + 2qy² = 4*qx² therefore: qx=±½√(1 + m00 - m11 - m22)	qxqy = ¼(m10+m01) gives: qx = (m10+m01)/(4qy)	qxqz = ¼(m02+m20) gives: qx = (m02+m20)/(4qz)
m02 - m20 = 2qxqz + 2qyqw - 2qxqz + 2qyqw m02 - m20 = 4qyqw therefore: qy = (m02 - m20)/( 4 *qw)	qxqy = ¼(m10+m01) gives: qy = (m10+m01)/(4qx)	1 + m11 - m00 - m22 = 1 + 1 - 2qx² - 2qz² - 1 + 2qy² + 2qz² - 1 + 2qx² + 2qy² = 4*qy² therefore: qy=±½√(1 + m11 - m00 - m22)	qyqz = ¼(m21+m12) gives: qy = (m21+m12)/(4qz)
m10 - m01 = 2qxqy + 2qzqw - 2qxqy + 2qzqw m10 - m01 = 4qzqw therefore: qz = (m10 - m01)/( 4 *qw)	qxqz = ¼(m02+m20) gives: qz = (m02+m20)/(4qx)	qyqz = ¼(m21+m12) gives: qz = (m21+m12)/(4qy)	1 + m22 - m00 - m11 = 1 +1 - 2qx² - 2qy² - 1 + 2qy² + 2qz² - 1 + 2qx² + 2qz² = 4*qz² therefore: qz=±½√(1 + m22 - m00 - m11)

metadata block

see also:	other conversations Euler Angles Matrix Rotations
Correspondence about this page	Open forum discussion Christian Ethan Paul Tim
Book Shop - Further reading. Where I can, I have put links to Amazon for books that are relevant to the subject, click on the appropriate country flag to get more details of the book or to buy it from them.

Maths - Conversion Matrix to Quaternion

Equations

Java Code

Simple Code

Code

Issues

C++ Code (kindly sent to me by Angel)

Alternative Method

Scaling

Rounding Errors

Derivation of Equations

Different Methods

Coordinate Systems

Spinor

Standards

Bilinear and Quadratic Forms

Rotation about a point other than origin

Example

Angle Calculator and Further examples

EuclideanSpace

Prerequisites

Matrix vs. Quaternion

Quaternion Papers