We are looking for a similar operation to union in set theory or the 'OR' operation in logic.
However such an operation would be non-linear and unstable. For example, if combining two vectors, the union would be these two vectors but not the vectors inbetween. How would we represent such a combination? We therefore change the definition slightly so that the join consists of the plane containing both vectors (both the vectors and the plane go through the origin).
Join Example
Lets start with the simple case of the basis vectors e1 and e2. The join is e1^e2 this is a plane and can't be simplified further.
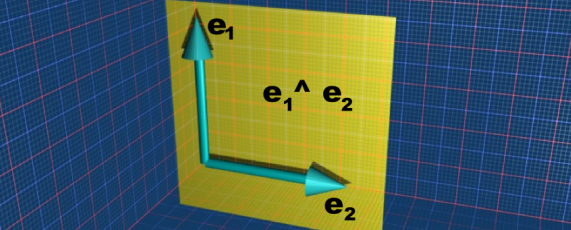
So how can we generalise this?
Duality of Meet and Join
We can calculate the meet if we know the join or visa-versa. However the dual depends on the blade being considered, this means we can't get an expression for the complete multivector.
(A
B)* = B* U A*
where:
- A,B are the two (different) bivectors.
- is the intersection (meet).
- U is the union (join).
- A* is the dual of A relative to the pseudoscalar of the subspace of the blade being considered.
Since the meet and join are both hard to calculate, this relationship does not necessarily help to calculate the join of a given blade.
Algorithm for calculating Join
It is easyest to calculate meet and join together, see meet page.
