Inverse
Here we look at the multiplicative inverse of multivector 'm', that is '1/m'. On this page we saw that the inverse of a pure vector is the same vector with a scaling factor.
Inverse of Bivector
On the same page we saw that the inverse of a bivector blade is calculated by replacing the bivector bases with their reverse (with a scaling factor). Taking the reverse of a bivector is the same as changing its sign. There is a problem in 4D and above though, the non-scalar terms may not cancel out because bivectors like e12 and e34 don't have a common term. So do four dimensional bivectors always have a multiplicative inverse?
Note on terminology: its not a good idea to use the division symbol '/' or '÷' because order is important for multivector multiplication, so when we write: a/b, is not clear if we mean a*(b-1) or (b-1)*a. However I will use the '/' symbol here with the understanding that it means: a/b = a*(b-1).
Lets try inverting the bivector: a e12 + b e34, this multiplying top & bottom by the reverse gives:
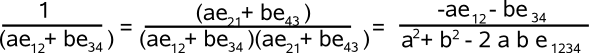
So the denominator still has a non-scalar term, we can make another attempt to cancel it out by multiplying by its reverse, so the numerator is,
(a e21 + b e43)(a² + b² + 2ab e1234)
= (a (a² + b²) - 2ab²) e21 + (b (a² + b²) - 2a²b) e43
= (a (a² - b²)) e21 + (b (b² - a²)) e43
= (a (a + b)(a - b)) e21 + (b (b - a)(b + a)) e43
and the denominator is:
(a² + b² - 2ab e1234)(a² + b² + 2ab e1234)
= (a + b)²(a² + b² - 2 a b)
so the result is:
= (a (a - b)/((a + b)(a² + b² - 2 a b))) e21
+ (b (b - a)/((a + b)(a² + b² - 2 a b))) e43
This looks very messy. Can it be simplified and further?
So how can we calculate the inverse for a general bivector based in 4D which contains up to 6 terms? The inverse of any two terms with a common term is the reverse, but if there is no common term the result is more complicated as we have seen.
The general case for the inverse of a 4D bivector:
1/ (a e12 + b e31 + c e23 + d e41 + f e42 + g e43)
is:
(-a e12 - b e31 - c e23 - d e41 - f e42 - g e43)(x - y e1234)/(x² - y²)
= ((g y -a x) e12
+ (f y - b x) e31
+ (d y - c x) e23
+ (c y - d x) e41
+ (b y - f x) e42
+ (a y - g x) e43)/(x² - y²)
where:
- x = a² + b² + c² + d² + f² + g²
- y =2*(a*g + b*f + c*d)
Inverse of 4D Trivector
1/(a e123 + b e142 + c e134 + d e324)
is equal to
(-a e123 - b e142 - c e134 - d e324)/(a² + b² + c² + d²)
So we don't have the same problem for trivectors that we had for bivectors, in 4d we can just use the reverse of all the terms, with the appropriate scaling factor.
Inverse of 4D Quadvector
1/(a e1234) = (1/a) e1234
There is only one quadvector in 4D which is its own inverse.
Dual
This multiplies by e1234 , for general information about n-dimensional dual see this page.
This is the bottom row of the multiplication table here.
Ar |
dual(Ar) = Ar* = e1234 Ar |
| e | e1234 |
| e1 | e1234 e1= e324 |
| e2 | e1234 e2= e134 |
| e3 | e1234 e3= e142 |
| e4 | e1234 e4= e123 |
| e12 | e1234 e12= e43 |
| e31 | e1234 e31= e42 |
| e23 | e1234 e23= e41 |
| e41 | e1234 e41= e23 |
| e42 | e1234 e42= e31 |
| e43 | e1234 e43= e12 |
| e123 | e1234 e123= e4 |
| e142 | e1234 e142= e3 |
| e134 | e1234 e134= e2 |
| e324 | e1234 e324= e1 |
| e1234 | e1234 e1234= e |
Reverse
The reverse function of a multivector reverses the order of its factors, including the order of the base values within a component. The reverse function is denoted by †, so the reversal of A is denoted by A†.
For general information about n-dimensional reverse see this page.
Ar |
Ar† |
| e | 1 |
| e1 | e1 |
| e2 | e2 |
| e3 | e3 |
| e4 | e4 |
| e12 | e21 = -e12 |
| e31 | e41 = -e31 |
| e23 | e32 = -e23 |
| e41 | e24= -e41 |
| e42 | e32= -e42 |
| e43 | e34= -e43 |
| e123 | e321= -e123 |
| e142 | e241 = -e142 |
| e134 | e431 = -e134 |
| e324 | e423 = -e324 |
| e1234 | e4321= e1234 |
The reversal function is important for a number of reasons, one reason is that it can map a multiplication into another multiplication with the order of the multiplicands reversed:
(A * B)† = B†* A†
We can think of this as a morphism where † maps to an equivalent expression with order of multiplication reversed.

Another application for the reversal function is to specify a transformation from one vector field to another:
pout = A pin A†
In other words, if pin is a pure vector (i.e. real, bivector and tri-vector parts are all zero) then pout will also be a pure vector. I would appreciate any proof of this.If you have a proof, that I could add to this page, please let me know, In the 3D case I guess I could try the brute force approach of multiplying out the terms for a general expression A and p.
I think this may also apply to:
pout = A pin A -1
but not every multivector is invertible, one condition that should ensure that a multivector is invertible is:
A A† = 1
Conjugate
The conjugate of Ar is denoted Ar~ where: Ar~*Ar = I = psudoscalar, for general information about n-dimensional conjugate see this page.
If Ar represents a transformation then Ar~ reverses the transformation
Ar |
Ar~=(Ar†)* | Ar~*Ar |
| e | (1)* = e1234 | e1234 |
| e1 | (e1)* = -e234 | e1234 |
| e2 | (e2 )* = e431 | e1234 |
| e3 | (e3 )* = -e124 | e1234 |
| e4 | (e4 )* = -e321 | e1234 |
| e12 | (-e12 )* = e34 | e1234 |
| e31 | (-e31 )* = e23 | e1234 |
| e23 | (-e23 )* = e42 | e1234 |
| e41 | (-e41 )* = e13 | e1234 |
| e42 | ( -e42)* = e14 | e1234 |
| e43 | ( -e43 )* = e12 | e1234 |
| e123 | ( -e123 )* = -e4 | e1234 |
| e142 | ( -e142 )* = e3 | e1234 |
| e134 | ( -e134 )* = e2 | e1234 |
| e324 | ( -e324 )* = e1 | e1234 |
| e1234 | ( e1234 )* = 1 | e1234 |
The last column confirms that Ar~*Ar = I = pseudoscalar.
Norm
under construction
Exponential
We define the exponential of multivector a as ea º åi=0¥ ai
/ i ! .
In particular:
ea is the traditional scalar exponential function
For any pure square multivector [ a2 = ±|a|2 ] we have ea = cos|a| + a~
sin|a| if a2 < 0 ;
cosh|a| + a~ sinh|a| if a2 > 0 ;
1+a if a2 = 0.
For unit multivector a:
eafeay = ea(f+y)
(d/df) elaf =lea(lf+p/2) =laelaf
Involution
a# = sum k=0(N (-1)k a <k> = a<+> - a<-> .
