Maths - Clifford Algebra - Meet

We are looking for a similar operation to intersection in set theory or the 'AND' operation in logic. This operation would be very useful, especially when we extend these operations to elements that don't necessarily go through the origin, for instance we could use it to test for collision detection.

However such an operation would be non-linear and unstable. For example, if comparing two vectors, the only common element would be the origin (represented by a scalar), unless the vectors were exactly equal, when the result would be this common input vector. If one of these vectors moved very slightly then the result would suddenly switch back to a scalar, this would not be very practical for practical applications because rounding errors would cause unpredictable switching between the scalar and vector outputs.

Meet Example

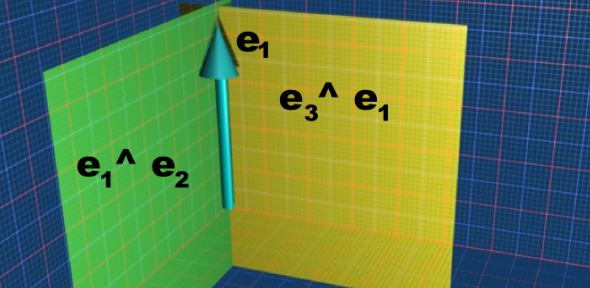
Lets start with the simple case of calculating the meet of two planes (in this example represented by the basis bivectors e₃^e₁ and e₁^e₂). The meet is e₁ we can see that this is the vector common to both planes. In other words, the meet of two planes is the line where they cross.

So how can we generalise this?

Duality of Meet and Join

We can calculate the meet if we know the join or visa-versa. However the dual depends on the blade being considered, this means we can't get an expression for the complete multivector.

(AB)^* = B^* U A^*

where:

• A,B are the two (different) bivectors.
• is the intersection (meet).
• U is the union (join).
• A^* is the dual of A relative to the pseudoscalar of the subspace of the blade being considered.

Since the meet and join are both hard to calculate, this relationship does not necessarily help to calculate the meet of a given blade.

Algorithm for calculating Meet

It seems to be very complicated to calculate the meet and join and I am struggling to understand it, I would welcome any help or ideas.

Here is an outline of the algorithm, note that it only combines two blades not whole multivectors. Let the two blades be A and B:

• If grade(A) > grade(B) swap A and B changing sign if necessary.
• calculate S=(A Δ B)^* where:
  • Δ = delta product
  • ^* = dual for this subspace.
• factorise S to give s_i
• calculate: reqM=required grade of meet and reqJ=required grade of join
• set M=1, J=I_n(I_n=is the pseudoscalar of the total space)
• for each s_i:
  • p_i = (s_i  A)  A^-1
  • r_i = s_i-p_i
  • where p_i is the projection of s_i and r_i is the rejection of s_i
  • If p_i≠0 M=M^p_i
  • if grade(M)=reqM then calculate J from M and break
  • otherwise continue with s_i+1
  • If r_i≠0 J=r_i  J
  • if grade(J)=reqJ then calculate M from J and break
  • otherwise continue with s_i+1

An algorithm for calculating Meet and Join is given at Ian Bells website.

Also see 'Gaigen' a Geometric Algebra progam here.

 

EuclideanSpace

home

Vector Dot Product

Conformal Geometry