Maths - 4D Clifford Algebra - Arithmetic

There is a 4D multivector calculator here.

The arithmatic on this page asumes the operands are a general case of a 4D multivector:

a.e + a.e1 e1 + a.e2 e2 + a.e3 e3 + a.e4 e4 + a.e12 e1^ e2 + a.e23 e2^ e3 + a.e31 e3^ e1 + a.e42 e4^ e2 + a.e41 e4^ e1+ a.e43 e4^ e3 + a.e123 e1^ e2^ e3 + a.e142 e1^ e4^ e2 + a.e134 e1^ e3^ e4 + a.e324 e3^ e2^ e4 + a.e1234 e1^ e2^ e3^ e4

and a second multivector:

b.e + b.e1 e1 + b.e2 e2 + b.e3 e3 + b.e4 e4 + b.e12 e1^ e2 + b.e23 e2^ e3 + b.e31 e3^ e1 + b.e42 e4^ e2 + a.e41 e4^ e1+ a.e43 e4^ e3 + b.e123 e1^ e2^ e3 + b.e142 e1^ e4^ e2 + b.e134 e1^ e3^ e4 + b.e324 e3^ e2^ e4 + b.e1234 e1^ e2^ e3^ e4

Adding multi vectors numbers

Just add each component independently as follows:

e = a.e + b.e
e1 = a.e1 + b.e1
e2 = a.e2 + b.e2
e3 = a.e3 + b.e3
e4 = a.e4 + b.e4
e12 = a.e12 + b.e12
e23 = a.e23 + b.e23
e31 = a.e31 + b.e31
e42 = a.e42 + b.e42
e41 = a.e41 + b.e41
e43 = a.e43 + b.e43
e123 = a.e123 + b.e123
e142 = a.e142 + b.e142
e134 = a.e134 + b.e134
e324 = a.e324 + b.e324
e1234 = a.e1234 + b.e1234

This operation will be coded in the multi4d class (see this class here).

When adding blades of different grade then we cant reduce it further and we leave the + in the number.

For example:

3 + 4 e1 + 5 e12

added to

5 + 4 e2 + 3 e12

gives

8 + 4 e1 + 4 e2 + 8 e12

Subtracting multi vectors numbers

Just subtract each component independently as follows:

e = a.e - b.e
e1 = a.e1 - b.e1
e2 = a.e2 - b.e2
e3 = a.e3 - b.e3
e4 = a.e4 - b.e4
e12 = a.e12 - b.e12
e23 = a.e23 - b.e23
e31 = a.e31 - b.e31
e42 = a.e42 - b.e42
e41 = a.e41 - b.e41
e43 = a.e43 - b.e43
e123 = a.e123 - b.e123
e142 = a.e142 - b.e142
e134 = a.e134 - b.e134
e324 = a.e324 - b.e324
e1234 = a.e1234 - b.e1234

This operation will be coded in the multi4d class (see this class here).

Multiplying 4D multivectors numbers (geometric product)

The main type of multiplication, which is described here, is geometric multiplication. Each term can be calculated using simple rules as described here.

In order to make sure we work out all possible combinations of products, I suggest using a table. The entries in the table only shows the type and sign change of the product, it does not show its absolute value. We therefore need to prefix the product by its numerical value which is the real number which is the product of the numbers at the top and left headings.

So we can start by entering the above results in the table, the value to the left of the * is represented by the columns and the value to the right of the * is represented by the rows. So when calculating a^b the column headings are denoted by a.?? and the rows are denoted by b.??

So the finished table is:

a*b
 b.e b.e1 b.e2 b.e3 b.e4 b.e12 b.e31 b.e23 b.e41 b.e42 b.e43 b.e123 b.e142 b.e134 b.e324 b.e1234
a.e e e1 e2 e3 e4 e12 e31 e23 e41 e42 e43 e123 e142 e134 e324 e1234
a.e1 e1 1 e12 -e31 -e41 e2 -e3 e123 e4 e142 -e134 -e23 -e42 e43 e1234 e324
a.e2 e2 -e12 1 e23 -e42 -e1 e123 e3 e142 -e4 e324 e31 e41 e1234 -e43 e134
a.e3 e3 e31 -e23 1 -e43 e123 e1 -e2 e134 e324 e4 -e12 e1234 -e41 e42 -e142
a.e4 e4 e41 e42 e43 1 -e142 e134 e324 -e4 e2 -e3 e1234 e12 e31 e23 -e123
a.e12 e12 -e2 e1 e123 -e142 -1 e23 -e31 e42 e41 e1234 e3 -e4 e324 -e134 e43
a.e31 e31 e3 e123 -e1 e134 -e23 -1 e12 -e43 -e1234 e41 e2 -e324 -e4 -e142 e42
a.e23 e23 e123 -e3 e2 e324 e31 -e12 -1 e1234 -e43 -e42 e1 e134 e142 -e4 e41
a.e41 e41 -e4 e142 e134 e1 -e42 e43 e1234 -1 e12 e31 e324 e2 -e3 e123 -e23
a.e42 e42 e142 e4 e324 -e2 -e41 -e1234 e43 -e12 -1 e23 -e134 e1 -e123 -e3 e31
a.e43 e43 -e134 e324 -e4 e3 e1234 -e41 e42 -e31 -e23 -1 -e142 e123 e1 -e2 -e12
a.e123 e123 -e23 -e31 -e12 -e1234 e3 e2 e1 -e324 e134 e142 -1 -e43 -e42 -e41 e4
a.e142 e142 -e42 e41 -e1234 e12 -e4 e324 -e134 e2 e1 -e123 -e43 -1 e23 -e31 e3
a.e134 e134 e43 -e1234 -e41 e31 -e324 -e4 e142 -e3 e123 e1 e42 -e23 -1 e12 e2
a.e324 e324 -e1234 -e43 e42 e23 e134 e142 -e4 -e123 -e3 -e2 e41 e31 -e12 -1 e1
a.e1234 e1234 -e324 -e134 e142 e123 e43 e42 e41 -e23 e31 -e12 -e4 -e3 -e2 -e1 1

In the above table we can see that some entries are commutative and some are anti-commutative, that is, if we swap rows and columns (or reflect in leading diagonal) some values remain the same and the others have their sign changed. We can also see that (A * B)† = B†* A† because if we rotate the whole table by 90 degrees then the entry will become its reversal.

I guess what we really need to know is that, given a multivector with numerical values: a.e, a.e1, a.e2, a.e3, a.e12, a.e31, a.e23 and a.e123 multiplied by a second multivector with numerical values: b.e, b.e1, b.e2, b.e3, b.e12, b.e31, b.e23 and b.e123 then what are the resulting numerical values. Multiplying out each term gives the following result:

e = +a.e*b.e+a.e1*b.e1+a.e2*b.e2+a.e3*b.e3+a.e4*b.e4-a.e12*b.e12-a.e13*b.e13-a.e14*b.e14-a.e23*b.e23
-a.e42*b.e42-a.e34*b.e34-a.e321*b.e321-a.e124*b.e124-a.e431*b.e431-a.e234*b.e234+a.e1234*b.e1234

e1 = +a.e*b.e1+a.e1*b.e-a.e2*b.e12-a.e3*b.e13-a.e4*b.e14+a.e12*b.e2+a.e13*b.e3+a.e14*b.e4+a.e23*b.e321
+a.e42*b.e124+a.e34*b.e431+a.e321*b.e23+a.e124*b.e42+a.e431*b.e34+a.e234*b.e1234-a.e1234*b.e234

e2 = +a.e*b.e2+a.e1*b.e12+a.e2*b.e-a.e3*b.e23+a.e4*b.e42-a.e12*b.e1-a.e13*b.e321+a.e14*b.e124+a.e23*b.e3
-a.e42*b.e4-a.e34*b.e234-a.e321*b.e13+a.e124*b.e14+a.e431*b.e1234-a.e234*b.e34-a.e1234*b.e431

e3 = +a.e*b.e3+a.e1*b.e13+a.e2*b.e23+a.e3*b.e-a.e4*b.e34+a.e12*b.e321-a.e13*b.e1-a.e14*b.e431-a.e23*b.e2
-a.e42*b.e234+a.e34*b.e4+a.e321*b.e12+a.e124*b.e1234-a.e431*b.e14-a.e234*b.e42-a.e1234*b.e124

e4 = +a.e*b.e4+a.e1*b.e14-a.e2*b.e42+a.e3*b.e34+a.e4*b.e-a.e12*b.e124+a.e13*b.e431-a.e14*b.e1-a.e23*b.e234
+a.e42*b.e2-a.e34*b.e3+a.e321*b.e1234-a.e124*b.e12+a.e431*b.e13-a.e234*b.e23-a.e1234*b.e321

e12 = +a.e*b.e12+a.e1*b.e2-a.e2*b.e1-a.e3*b.e321+a.e4*b.e124+a.e12*b.e-a.e13*b.e23+a.e14*b.e42+a.e23*b.e13
-a.e42*b.e14-a.e34*b.e1234-a.e321*b.e3+a.e124*b.e4+a.e431*b.e234-a.e234*b.e431-a.e1234*b.e34

e13 = +a.e*b.e13+a.e1*b.e3+a.e2*b.e321-a.e3*b.e1-a.e4*b.e431+a.e12*b.e23+a.e13*b.e-a.e14*b.e34-a.e23*b.e12
-a.e42*b.e1234+a.e34*b.e14+a.e321*b.e2+a.e124*b.e234-a.e431*b.e4-a.e234*b.e124-a.e1234*b.e42

e14 = +a.e*b.e14+a.e1*b.e4-a.e2*b.e124+a.e3*b.e431-a.e4*b.e1-a.e12*b.e42+a.e13*b.e34+a.e14*b.e-a.e23*b.e1234
+a.e42*b.e12-a.e34*b.e13+a.e321*b.e234-a.e124*b.e2+a.e431*b.e3-a.e234*b.e321-a.e1234*b.e23

e23 = +a.e*b.e23-a.e1*b.e321+a.e2*b.e3-a.e3*b.e2+a.e4*b.e234-a.e12*b.e13+a.e13*b.e12-a.e14*b.e1234+a.e23*b.e
+a.e42*b.e34-a.e34*b.e42-a.e321*b.e1+a.e124*b.e431-a.e431*b.e124+a.e234*b.e4-a.e1234*b.e14

e42 = +a.e*b.e42-a.e1*b.e124-a.e2*b.e4+a.e3*b.e234+a.e4*b.e2+a.e12*b.e14-a.e13*b.e1234-a.e14*b.e12-a.e23*b.e34
+a.e42*b.e+a.e34*b.e23-a.e321*b.e431-a.e124*b.e1+a.e431*b.e321+a.e234*b.e3-a.e1234*b.e13

e34 = +a.e*b.e34-a.e1*b.e431+a.e2*b.e234+a.e3*b.e4-a.e4*b.e3-a.e12*b.e1234-a.e13*b.e14+a.e14*b.e13+a.e23*b.e42
-a.e42*b.e23+a.e34*b.e+a.e321*b.e124-a.e124*b.e321-a.e431*b.e1+a.e234*b.e2-a.e1234*b.e12

e321 = +a.e*b.e321-a.e1*b.e23+a.e2*b.e13-a.e3*b.e12+a.e4*b.e1234-a.e12*b.e3+a.e13*b.e2-a.e14*b.e234-a.e23*b.e1
+a.e42*b.e431-a.e34*b.e124+a.e321*b.e+a.e124*b.e34-a.e431*b.e42+a.e234*b.e14-a.e1234*b.e4

e124 = +a.e*b.e124-a.e1*b.e42-a.e2*b.e14+a.e3*b.e1234+a.e4*b.e12+a.e12*b.e4-a.e13*b.e234-a.e14*b.e2-a.e23*b.e431
-a.e42*b.e1+a.e34*b.e321-a.e321*b.e34+a.e124*b.e+a.e431*b.e23+a.e234*b.e13-a.e1234*b.e3

e431 = +a.e*b.e431-a.e1*b.e34+a.e2*b.e1234+a.e3*b.e14-a.e4*b.e13-a.e12*b.e234-a.e13*b.e4+a.e14*b.e3+a.e23*b.e124
-a.e42*b.e321-a.e34*b.e1+a.e321*b.e42-a.e124*b.e23+a.e431*b.e+a.e234*b.e12-a.e1234*b.e2

e234 = +a.e*b.e234+a.e1*b.e1234+a.e2*b.e34+a.e3*b.e42+a.e4*b.e23+a.e12*b.e431+a.e13*b.e124+a.e14*b.e321+a.e23*b.e4
+a.e42*b.e3+a.e34*b.e2-a.e321*b.e14-a.e124*b.e13-a.e431*b.e12+a.e234*b.e-a.e1234*b.e1

e1234 = +a.e*b.e1234+a.e1*b.e234+a.e2*b.e431+a.e3*b.e124+a.e4*b.e321+a.e12*b.e34+a.e13*b.e42+a.e14*b.e23+a.e23*b.e14
+a.e42*b.e13+a.e34*b.e12-a.e321*b.e4-a.e124*b.e3-a.e431*b.e2-a.e234*b.e1+a.e1234*b.e

Inner and Outer products

trasitions

In addition to the geometric product there are two more types of multiplication used in Geometric Algebra. These extend and generalise the 'dot' and 'cross' products used in 3D vector algebra.

Inner product by a vector reduces the grade of a multivector. It is related to the dot product.

Outer product by a vector increases the grade of a multivector. It is related to the cross product.

4D Outer multiplication table

a*b
 b.e b.e1 b.e2 b.e3 b.e4 b.e12 b.e31 b.e23 b.e41 b.e42 b.e43 b.e123 b.e142 b.e431 b.e324 b.e1234
a.e e e1 e2 e3 e4 e12 e31 e23 e41 e42 e43 e123 e142 e431 e324 e1234
a.e1 e1 0 e12 -e31 -e41 0 0 e123 0 e142 -e134 0 0 0 e1234 0
a.e2 e2 -e12 0 e23 -e42 0 e123 0 e142 0 e324 0 0 e1234 0 0
a.e3 e3 e31 -e23 0 -e43 e123 0 0 e134 e324 0 0 e1234 0 0 0
a.e4 e4 e41 e42 e43 0 -e142 e134 e324 0 0 0 e1234 0 0 0 0
a.e12 e12 0 0 e123 -e142 0 0 0 0 0 e1234 0 0 0 0 0
a.e31 e31 0 e123 0 e134 0 0 0 0 -e1234 0 0 0 0 0 0
a.e23 e23 e123 0 0 e324 0 0 0 e1234 0 0 0 0 0 0 0
a.e41 e41 0 e142 e134 0 0 0 e1234 0 0 0 0 0 0 0 0
a.e42 e42 e142 0 e324 0 0 -e1234 0 0 0 0 0 0 0 0 0
a.e43 e43 -e134 e324 0 0 e1234 0 0 0 0 0 0 0 0 0 0
a.e123 e123 0 0 0 -e1234 0 0 0 0 0 0 0 0 0 0 0
a.e142 e142 0 0 -e1234 0 0 0 0 0 0 0 0 0 0 0 0
a.e143 e143 0 -e1234 0 0 0 0 0 0 0 0 0 0 0 0 0
a.e324 e324 -e1234 0 0 0 0 0 0 0 0 0 0 0 0 0 0
a.e1234 e1234 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

4D Inner multiplication table

a*b
 b.e b.e1 b.e2 b.e3 b.e4 b.e12 b.e31 b.e23 b.e41 b.e42 b.e43 b.e123 b.e142 b.e134 b.e324 b.e1234
a.e 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
a.e1 0 1 0 0 0 e2 0 -e3 -e4 0 0         e324
a.e2 0 0 1 0 0 -e1 e3 0 0 -e4 0         e134
a.e3 0 0 0 1 0 0 -e2 e1 0 0 -e4         -e142
a.e4 0 0 0 0 1 0 0 0 e1 e2 e3         -e123
a.e12 0 -e2 e1 0 0 -1                   e43
a.e31 0 0 -e3 e2 0   -1                 e42
a.e23 0 e3 0 -e1 0     -1               e41
a.e41 0 e4 0 0 -e1       -1             -e23
a.e42 0 0 e4 0 -e2         -1           e31
a.e43 0 0 0 e4 -e3           -1         -e12
a.e123 0                     -1       e4
a.e142 0                       -1     e3
a.e134 0                         -1   e2
a.e324 0                           -1 e1
a.e1234 0 -e324 -e134 e142 e123 e43 e42 e41 -e23 e31 -e12 -e4 -e3 -e2 -e1 1

 

 

Division

We don't tend to use the 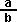divide notation for division, since multivector multiplication is not commutative we need to be able to distinguish between [a][b]-1 and [b]-1[a]. So instead of a divide operation we tend to multiply by the inverse.

So the problem is, how to calculate the inverse of a multivector, this is discussed here.

4D Multivector Calculator

The following calculator allows you to calculate multivector arithmetic. Enter the values into the top two multivectors and then press "+ - or * " to display the result in the bottom multivector:

scalar e          
vector e1 e2 e3 e4    
bivector e12 e13 e14 e23 e42 e34
tri-vector e321 e124 e431 e234    
quad-vector e1234            
scalar e          
vector e1 e2 e3 e4    
bivector e12 e13 e14 e23 e42 e34
tri-vector e321 e124 e431 e234    
quad-vector e1234            
=
scalar e          
vector e1 e2 e3 e4    
bivector e12 e13 e14 e23 e42 e34
tri-vector e321 e124 e431 e234    
quad-vector e1234            
metadata block
see also:

 
Correspondence about this page

Book Shop - Further reading.

Where I can, I have put links to Amazon for books that are relevant to the subject, click on the appropriate country flag to get more details of the book or to buy it from them.
flag flag flag flag flag flag Clifford Algebra to Geometric Calculus: A Unified Language for Mathematics and Physics (Fundamental Theories of Physics). This book is intended for mathematicians and physicists rather than programmers, it is very theoretical. It covers the algebra and calculus of multivectors of any dimension and is not specific to 3D modelling.

 

flag flag flag flag flag flag New Foundations for Classical Mechanics (Fundamental Theories of Physics). This is very good on the geometric interpretation of this algebra. It has lots of insights into the mechanics of solid bodies. I still cant work out if the position, velocity, etc. of solid bodies can be represented by a 3D multivector or if 4 or 5D multivectors are required to represent translation and rotation.

 

Terminology and Notation

Specific to this page here:

 

This site may have errors. Don't use for critical systems.

Copyright (c) 1998-2023 Martin John Baker - All rights reserved - privacy policy.