Abstract
This page is about how geometric algebra can represent objects in three dimensions and some useful concepts for analysing 3D geometry.
To see how the same concepts can be described using more conventional vector algebra see this page.
This page assumes an understanding of coordinate systems described here, you may also want to review rotations .
Points and Lines from the Origin
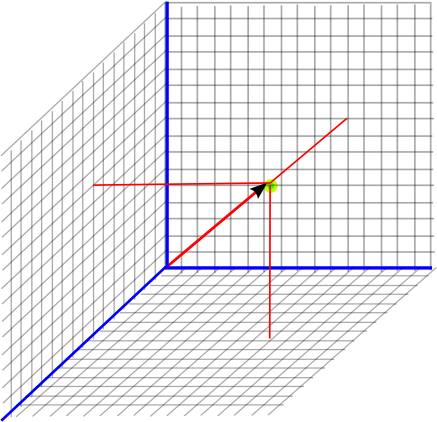
We can use a 3 dimensional vector to represent a displacement from the origin and therefore specify a given point by showing its displacement from the origin. For instance, the point shown below is 9 up, 11 right and 7 toward viewer, which can be represented by the vector (11,9,7). By convention the x coordinate is shown first, then the y coordinate, then the z coordinate.
Angles
In 3 dimensions rotations have 3 degrees of freedom as described here. For instance we can define an angle to rotate the red vector to the blue vector in the diagram below:
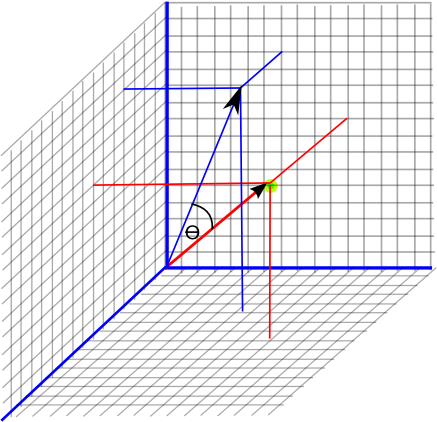
Just defining the angle is not enough as we have to define the direction that it rotates, we can use a vector to do this, one way to do this is to define an axis which we are rotating around. We can do this because in 3 dimensions lines and planes are 'duels' that is every line has a corresponding plane and visa-versa. More generally we can define the direction of rotation by defining a plane, points in that plane when rotated, stay in that plane.
If we ignore the direction of the rotation, the angle will be,
angle = acos(real(v1*v2))
where:
- real() = function which returns the scalar component and sets the vector, bivector and tri-vector components to zero.
- v1 = vector (scalar, bivector and tri-vector components are zero)
- v2 = vector (scalar, bivector and tri-vector components are zero)
- * = geometric product (see this page for definition)
Areas
In 3 dimensions there are two ways to define areas:
- As a scalar quantity which defines the total surface area of an object (for example: how much paper it would take to wrap it).
- The area of a slice through the object, this requires a 3D vector to define it because we need to know the direction.
This second case is known as a 'directed area'
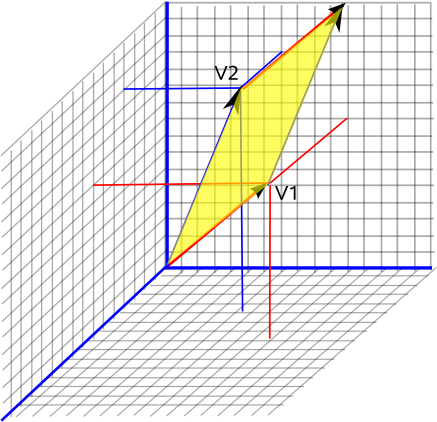
As an example of a directed area, what is the area of a diamond shape with two sides = V1 and two sides = V2 as shown in the diagram above. The answer is:
directed area = vector(V1 * V2)
where:
- vector() = function which returns the vector and sets scalar, bivector and tri-vector components to zero.
- v1 = vector (scalar, bivector and tri-vector components are zero)
- v2 = vector (scalar, bivector and tri-vector components are zero)
- * = geometric product (see this page for definition)
As explained already, it just so happens that in 3 dimensions we can represent a directed area with a 3 dimensional vector. Or more correctly a bivector because it has slightly different properties in that the result of cross product with bivector operands can be reversed in certain circumstances. bivectors are explained on this page.
If we want to define a plane, without defining an area of it, we can use a normalised (unit length) bivector.
Directed areas can be used to define the direction of rotation explained above. We could use the direction of the bivector to define the plane and the length of the bivector to define the angle, in this way the the bivector alone can fully define a rotation. A more common way to define the rotation is to use a quaternion, which makes it easier to combine rotations, this is related to the angle and the bivector as follows:
real part of quaternion = cos(angle/2)
imaginary part of quaternion = sin(angle/2) * bivector
Volume
A volume, in 3 dimensional space, is a single scalar quantity. This might, for example, indicate how much space is taken up by an object.
Where next
To see how these objects can be projected onto other objects read this page.
