Maths - Topological Space

Topological Space

We can think of topology as a generalisation of geometry where we no longer have to use the concept of distance (metric space). Topology has other, more general concepts of nearness. Topology does not to be geometric though, it is applicable in many situations where concepts such as neighborhood, convergence and continuity can be used. For example sequences and recursively defined structures in computer science.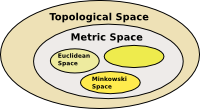

So topology links together many aspects of mathematics such as set theory, logic and geometry.

We start with geometry because our human intuition can best understand concepts like neighborhood, convergence and continuity in geometric terms. So, for instance we can study 'rubber sheet geometry' or the properties of manifolds that are preserved by continuous maps.

To do this we use the concept of 'open space' and 'open set'. The notion of an open set provides a way to speak of distance in a topological space, without explicitly defining a metric on the space. Although one cannot obtain concrete values for the distance between two points in a topological space, one may still be able to talk about 'nearness' in the space, thus allowing concepts such as continuity to translate into the theory of open sets.

Topological Spaces

We can either define topological spaces in terms of neighbourhoods or, in terms of sets, in a combinatorial way.

So we can think of it as consisting of multiple open sets, each of which may contain multiple points. A point may appear in multiple open sets. There are other rules described below.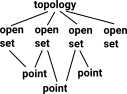

A topological space is defined by an ordered pair (X,τ) where:

X is a set
τ (Greek letter tau) is a collection of subsets of X, each of these subsets is called an open set.

We can think of τ as either:

A subset of the powerset of X.
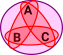
- τ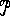(X)
or a collection of open sets.

So far this topological space seems very similar to simplicial complexes (discussed on the page here). However there are 3 additional constraints which must be true for this to be a topological space:

X and Ø are elements of τ.
τ is closed under finite intersections.
τ is closed under arbitrary unions.

These are quite restrictive requirements but, if they are met, a topological space has a concept of nearness without the requirement for a metric space.

Examples of Topological Spaces

discrete and trivial are two extremes:

trivial topology

The only open sets are the empty set Ø and the entire space.

Each of the elements of X, that is 'a', 'b' and 'c', only occur is sets with all the other elements. This means that the elements are indistinguishable from each other and therefore every element is in the neighbourhood of every other element.

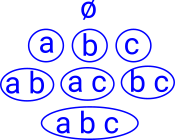discrete topology

The open sets are the whole power set so it contains all possible subsets.

Every element of X appears in every combination with every other element. This means that there are no neighbourhoods so every element is separated from the rest.

On the page here we discuss simplicies, this is also a set with all subsets, so a simplex is a discrete space.

The interesting topologies are between these extremes.

Although a simplex is a topological space, when they are glued together to form a cell complex, a complex is not necessarily a topological space.

Representations of Topological Space

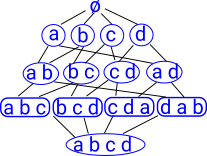
Birkhoff's representation theorem (Wiki) The theorem can be interpreted as providing a one-to-one correspondence between distributive lattices and partial orders, or between finite topological spaces and preorders. The top diagram (Venn diagram Wiki) shows the same information as the diagram below it (Lattice diagram Wiki). The lines in this lattice diagram represent a subset relationship. So far we have not shown neighbourhoods.

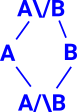The elements of any finite distributive lattice can be represented as finite sets, in such a way that the lattice operations correspond to unions and intersections of sets.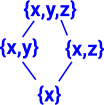
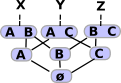
So how can we represent neighbourhoods? To investigate this lets look at a different topology shown in the lattice here: Neighbourhoods are given by sets of elements of X that only occur is sets with all the other elements. This means that the elements are indistinguishable from each other and therefore every element is in the neighbourhood of every other element.
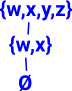So, in this case, w and x are in the same neighbourhood and y and y are in the same neighbourhood.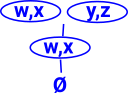
A better diagram to indicate that might be this diagram: In this case the lines link elements in the same neighbourhood.

Alexandrov Topology and Preorders

A preorder is:

A reflexive and transitive algebra.
A category where there is at most one morphism going from any object a to any object b.
Every preorder can be given a topology, the Alexandrov topology. - Wiki.

Every preorder on a set is in one-to-one correspondence with an Alexandrov topology on that set.

In an Alexandrov space let x₁≤x₂ if U₁≤U₂

where:

U₁≤U₂ means the open set U₁is a subset of the open set U₂

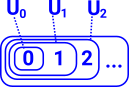Preorders may be used to define interior algebras. an interior algebra is a certain type of algebraic structure that encodes the idea of the topological interior of a set. Interior algebras are to topology and the modal logic S4 what Boolean algebras are to set theory and ordinary propositional logic. - Wiki.

Maps From The Interval

A real interval is a set of real numbers between two given endpoints (wiki).

This be generalised to an a non-metric, more discrete topology.

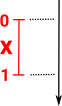We can apply constraints in the form of equations, for instance to get a circle with a distinguished point 'p':

p = X(0) = X(1)

Path

A path in a topological space T is a continuous map Γ from [0,1] to T:

Γ: [0,1] -> T

see this site

Loop

A path is a loop if Γ(0) = Γ(1)

Homotopy

A homotopy is a continuous map from the product of intervals to the topological space (with certain proporties).

[0,1] × [0,1] -> T

see homotopy page

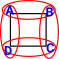
Can we Represent a Circle?

If the Alexandrov topology is a preorder then can it represent a loop (circle) without constraints (equations)?

All finite topologies are Alexandrov topologies (the distinction between topological spaces and Alexandrov topological spaces only makes a difference for infinite sets).

We can represent a circle with infinite (based on real numbers) sets but can we represent a circle with finite sets?

Attempt to represent a circle:

Here there is no connection between {a} and {c} or {a,b} and {c,d} for example so not all subsets are included.

So this is not a valid topological space.

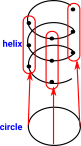
Could we code a helix as a line using Alexandrov space as described above.

Then take another topology by identifying points on the same part of the circle.

Then take the quotient of these two topological spaces?

Topological Space and W-types

Are the structures of topological Spaces (especially Alexandrov topology) and W-types related in some way?

They both seem to be able to code linear structures and trees but not loops (circles).

Open Sets in Abstract Topological Spaces

These subsets of X are open sets (see page here about open sets) because:

Both X and Ø are open sets
Any union of open sets is an open set
Any finite intersection of open sets is an open set

Caution, these topologies need to be in the same space.

Intuitivly we can think of closed or open sets as containing or not containing their boundary points:

A set is open if it does not contain its boundary points.
A set is closed if and only if it contains all of its boundary points.

Subdividing Space

Sometimes, in mathematics, we deal with objects that are unbounded: we can keep increasing them indefinitely. For example, we could start with the quantity 1 then add one to that, then add one to that, and so on. If we take the limit to this we get infinity.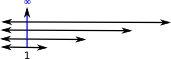

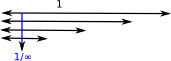Topology seems to be concerned more with the other direction, that is, if we start with a quantity (say 1) and then keep dividing it there is a infinitesimally small limit.

So subdividing an object is an important concept in topology.

Subtopologies

We can generate sub-topologies τ' by taking a subset of the set X. The induced topology is:

τ' = (τX')

Hausdorff Spaces

Topology has historically arisen from geometry, typically geometric situations use the 'Housdorff separation axiom'. Applications in computer science tend to be non-Hausdorff.

Hausdorff - geometric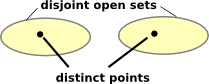

This defines the opposite of nearness (distinct points)

non-Hausdorff - computer science

(approximation)

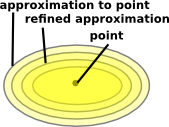This defines nearness.

A topological space is said to be a Hausdorff space if given any pair of distinct points p₁, p₂H, there exists neighborhoods U₁ of p₁ and U₂ of p₂ with U₁U₂ = Ø.

In other words: disjoint open sets separate points.

Basis and Subbasis

A base (or basis) B for a topological space X with topology τ is a collection of open sets in τ such that every open set in τ can be written as a union of elements of B. We say that the base generates the topology τ.

Every open set is a union of basis elements.
Every open set is a union of finite intersections of subbasis elements.

Morphisms between Topological Spaces

The most important part of this subject is the relationship between different topologies. The mappings or morphisms between them.

For example, the continuous 'rubber geometry' deformations as between a toroid and a mug.

There are two related mapping types continuous mappings and homeomorphisms.

For more detail see page here.

Fibre Bundles and Sheaves

The concept of a 'fibre bundle' allows us to define some structure to subsets of a space and the 'sheaf' concept adds more structure.

Topology allows us to look at mappings of points (shown at the top of this diagram) and the mapping between neighborhoods (open sets).

The mapping between the logic of open sets is in the reverse direction (contravarient) and defines the continuity.

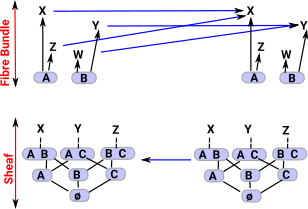If I is a set: I=set{A,B,C,D}
then a bundle is denoted Bn(I) or setI
Wheredenotes a comma category.

Fibre bundles are discussed on this page.

Topology	Category	Objects	Morphisms	Logic
Fibre Bundle	BN(I) equivalent to comma category: setI	pairs: (A,f) where f:A->I	(A,f) -> (B,g) preserves meets and joins	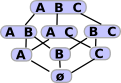all subsets of I
sheaf	TOP(I)		preserves meets and joins and subsets (implication) that is Heyting algebra.	open subsets of I

Topological Space and Simplicial Sets (Geometric Realisation)

Topological spaces have some nice properties, they have the concept of nearness in the most general way. However topological spaces have some quite stringent requirements, geometric realisation gives use a way to embed any CW complexes or simplicial set as a topological space.

A first thought for how to embed simplicial sets in topological spaces might be to equate each simplex with an open set, unfortunately this won't work for the following reasons:

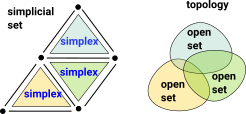Every union of simplices in a CW complex is not a simplex but unions of open sets must be open sets.
Every pair of simplices don't necessarily have an intersection.

There is a way to canonically get a topological space from a simplicial complex, this requires a much higher dimensional space so its not very intuitive. For instance, to encode a graph (2D complex), each vertex in the graph needs to have its own dimension in the topological space.

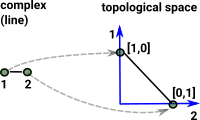
Here we want to encode a complex with two points and a line. We embed this in 2 dimensional Euclidean space (and therefore topological space).

Each of the points is now a vector in its own dimension, these are [1,0] and [0,1] and they are the basis vectors.

The line is a straight line between these basis vectors, parameterised by t like this { (1-t)*[1,0]+t*[0,1] | t[0,1] }.

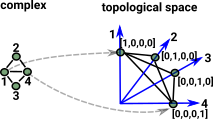A more complex graph gives a lot more dimensions which makes visualising the topological space harder.

For more information about geometric realisation see the page here.

metadata block

see also:	Set theory
Correspondence about this page
Book Shop - Further reading. Where I can, I have put links to Amazon for books that are relevant to the subject, click on the appropriate country flag to get more details of the book or to buy it from them.	Introduction to Topological Manifolds (Graduate Texts in Mathematics S.) Other Books about Curves and Surfaces