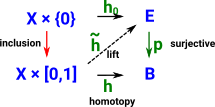Fibres and fibre bundles are an important mathematical structure that occurs across many branches of maths. Therefore there are many ways to approach this subject:
- Topology and Open Sets.
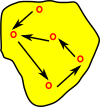
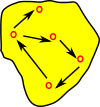
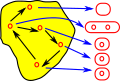
- Set Theory - On these pages we discuss how reversing a surjective map generates this structure.
- Type Theory - On these pages we look at this structure as a type family or a disjoint set of types indexed by another type.
- Category Theory
Introduction
A homotopy equivalence is a looser form of 'same shape' than a homeomorphism.
| There are continuous maps that are not allowed in a homeomorphism. For example, a line can be continuously contracted down to a point but that would not be allowed in a homeomorphism because the reverse mapping would not take every point back to itself. |  |
As Fibre Bundle
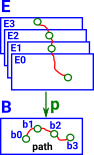
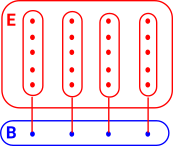
A fibre bundle is a set of lines/links between a base space B and a total space E. These link elements of B with, possibly multiple, elements of E. This is a continuous surjective map. This forms a space that is locally a product space, but globally may have a different topological structure (see Wikipedia page). |
 |
Inverse Functions
Fibrations
The notion of a fibration generalizes the notion of a fiber bundle (see Wikipedia page)
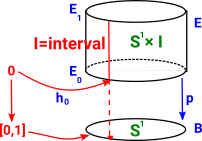
Fibrations have additional structure to fiber bundles which allows some structure in B to be 'lifted' to E. See the page here for an introduction.
Fibration and Co-fibration
Homotopy has the concept of:
- a fibration which has the lifting property.
- a co-fibration which has the extension property -extension is dual to lift.
Fibration |
Co-fibration (Extension Property) |
|
|---|---|---|
| Homotopy | Fibration |
Co-fibration (see page here) |
Combinatorics |
Kan fibration (see page here) |
Kan extension (see page here) |
Kan fibrations are combinatorial analogs of Serre fibrations of topological spaces.
Fibre Bundle as Dependent TypeIn type theory dependent types are where there is a family of types indexed by elements of another type. More about this relation to type theory on the page here.
|
 |
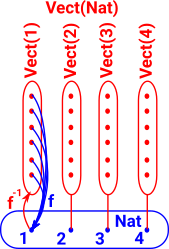Example - Fibre Bundle as Endo Function
| C |  |
Every element has 1 outgoing arrow. May have zero or multiple incoming arrows. |
| Cop |  |
Every element has 1 incoming arrow. May have zero or multiple outgoing arrows. |
| Cop->set |  |
Every element maps to a set. |
This page explains Fibre bundles.
Example - Fibre Bundle as Database
More about this on page here.
Fibre as a Pullback
Subset
If we take a subset of the function before inverting it we get a pullback.
Hence we have two morphisms to C so this looks like the given part of a pullback. |
 |
|
 |
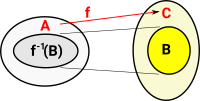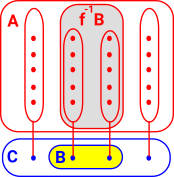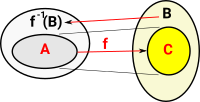
So the structure in A relates to the structure in C. | |
| To complete the square we add cone for this diagram and we call it f-1(B) to emphasise that it is the inverse of 'f'. |  |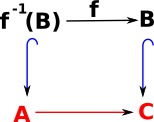
|
Superset
What if we do the opposite and take a superset of A rather than taking a subset of it? The function 'f' is only defined from A to C so we need to find some way to extend it to handle the bigger set. To do this we need to get some information about the bigger set by knowing something about the wider structure. For instance if we have a sheaf. See Kan extension page. |
 |
More about pullbacks in catagory theory section on page here.
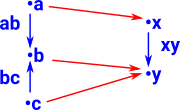
Fibre With StructureThe examples so far show how reversing a map between sets gives some interesting structures. What if we start with sets which already have some structure? The diagram on the right is intended to show a morphism between partial orders. So the blue arrows represent ≥and the arrow 'ab' means b ≥ a. The red arrows show the morphism between the partial orders and these all need to play nicely together. |
 |
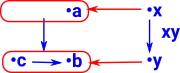
So how can this morphism be reversed? The diagram on the right is the best I can do although somehow it doesn't seem completely correct, for instance it seems to imply that c ≥ a whereas the original diagram above doesn't imply that. In order to be consistent this morphism needs to be a local homeomorphism which is a function between topological spaces that preserves local but not necessarily global structure. The interesting thing is that this is dividing the structure into 'local' structure and 'global' structure. For more information about this see the page about sheaves. |
 |
A fibre as a projection.The simple case on the right is intended to show a projection of a three dimensional object onto a two dimensional surface. This is just a projection from a product space. However a projection along a fibre is more general than that, locally it still looks like a product space, but globally it can look very different. |
 |
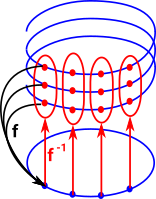
A standard example of this is a helix, which can be projected onto a circle since any local section corresponds to a section of a circle. Locally a section of the spiral looks like a section of the circle, globally the circle and the spiral are different. To reverse the direction of this projection we have to create a set (type) of points. |
 |
| A similar example is the Möbius band being mapped onto a cylinder. |  |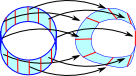
Fibration
We can generalise a fibre bundle to have more structure than a type indexed by a set:
- A fibration allows us to use something more complicated than a set to index types.
- A sheaf allows us to relate local and global structure.
FibrationIn this diagram B represents the base space and E represents the total space. B is now more than the index set because it now has structure. p is a projection of the total space into the base space. |
 |
|
 |
The diagram needs to have the lifting property which says that there must be an arrow h~ from the path to E. So given the structure in E0 we can get the structure at other points. |
|
Fibration ExampleA cylinder (S1*I) mapped onto a circle (S1). This map is a projection locally (upto homeomorphism). Since we only require a projection locally we could also project from a helix or a Möbius band. |
 |
|
Fibrations of Graphs
theory: topological graph theory
| undirected graph: | covering projection |
| directed graph: | fibration (weaker form of covering projection) |
Here is an example for directed multigraphs. Each node in the top graph maps to the bottom graph (fibration). The corresponding node always has the same number and colour of incoming arcs (but not necessarily outgoing arcs). This gives some sort of local invariance. |
 |
Sheaves
Sheaves add extra structure to fibrations, so instead of just Set we now have:
Cop->Set
Where Cop gives the structure and Set holds the data.
This is known as a presheaf, to make this into a sheaf we need to be able to glue these elements of structure together.
Computation, Logic and Geometry
Venn diagrams show us a deep connection between sets , logic and geometry. If we swap from sets to types and and from Boolean logic to constructive logic we get similar mathematical structure that has this 3-way correspondence. |
 |
| Type Theory | Logic | Geometry | |
|---|---|---|---|
| types |
|
|
|
| terms |
constants, variables & functions. |
a term is a proof of the proposition. |
|
| non-dependant types | empty  |
false | initial object |
| unit T | true | terminal object | |
| sum | or | coproduct | |
| pair | and | product | |
| function | implication | internal hom | |
| dependant types | type family | predicate | bundle |
| substitution | substitution | pullback of a bundle | |
| Σ type | exists | total space of a bundle | |
| Π type | for all | space of sections of bundles |
