On this page we look at topological aspects of simplicial complexes such as boundaries and cycles.
The algorithms here assume that the simplexes (faces) are wound in a consistent way. To illustrate this we will take an example:
Here we have two triangles joined by an adjacent side. The arrows show the order that the vertices indexes are listed. It is important that they are defined in a consistent way. Here all triangles go anticlockwise. So the arrows on the adjacent line go in opposite directions. We interpret this as allowing us to cancel out these arrows. This leaves the boundary shown in red: |
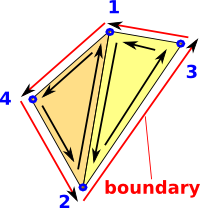 |
We can use the code to do this as follows:
(1) -> ASIMP := FiniteSimplicialComplex(VertexSetAbstract)
(1) FiniteSimplicialComplex(VertexSetAbstract)
Type: Type
(2) -> v1:List(List(NNI)) := [[1::NNI,2::NNI,3::NNI],[4::NNI,2::NNI,1::NNI]]
(2) [[1,2,3],[4,2,1]]
Type: List(List(NonNegativeInteger))
(3) -> sc1 := simplicialComplex(vertexSeta(4::NNI),v1)$ASIMP
+1 2 3+
(3) | |
+4 2 1+
Type: FiniteSimplicialComplex(VertexSetAbstract)
(4) -> boundaryLine(sc1)$ASIMP
+2 3+
| |
|3 1|
(4) | |
|4 2|
| |
+1 4+
Type: FiniteSimplicialComplex(VertexSetAbstract)
|
In the case of a single line, it will not have a boundary because it does not enclose any area. As shown here:
(5) -> v2:List(List(NNI)) := [[1::NNI,2::NNI]]
(5) [[1,2]]
Type: List(List(NonNegativeInteger))
(6) -> sc2 := simplicialComplex(vertexSeta(2::NNI),v2)$ASIMP
(6) [1 2]
Type: FiniteSimplicialComplex(VertexSetAbstract)
(7) -> boundaryLine(sc2)$ASIMP
(7) []
Type: FiniteSimplicialComplex(VertexSetAbstract) |
Homology