Not sure what the 'W' stands for, could be from the Martin-Löf concept of 'well orderings'. I think its a 'W' and not omega. Though it seems related to 'ω-complete partial order' (see cpo) from denotational semantics/domain theory.
In category theory this is an initial algebra for a polynomial endofunctor.
In type theory it is a free term algebra.
Examples
An important example is the natural numbers. They can be defined in terms of Peano algebra. This is not very practical for everyday use but has nice properties for proving things about natural numbers. |
Idris Codedata Nat = Z // Zero | S Nat // Successor. |
| The natural number example has two constructors, Zero (arity 0) and Successor (arity 1). Lets explore what happens when we add more constructors. For instance lets have two constructors of arity 1. | Idris Codedata MyType = Z | X MyType | Y MyType |
This generates 'words', starting with Z and then any sequence of X and Y. So a W-type is a tree structure. There is no restriction on the order or length of the terms. This is known as a 'free' algebra. |
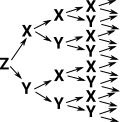 |
We could add additional constructors of arity 1 to increase the types of characters in the words. Another thing we could do is add constructors of arity 2 and above. |
Idris Codedata MyType = Z | X MyType | Y MyType | U MyType MyType |
This seems to allow us to join arrows. So we appear to be able to construct lattices although I cant see a way to limit the construction to a lattice because we can always have paths going off in all directions. |
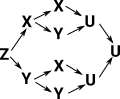 |
Logic of W-types
The terms/elements of a W-type can be considered to be “rooted well-founded trees” with a certain branching type.
In the table below:
|
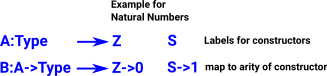 |
So if a is an element of A, that is an individual constructor label, then B(a) is the arity for that constructor.
Introduction
In a programming language a constructor would look something like this:
name(parameter1, parameter2)
or in a functional language like this:
(name parameter1 parameter2)
In the case of a W-type the parameters are all the same as the type being constructed so all we need to know is the number of parameters.
So (W a : A)B(a) is a W-type.
Elimination
Elimination is usually a way to prove properties of W.
For example, for natural numbers: |
nat_induction :
(prop : Nat -> Type) -> -- Property to show
(prop Z) -> -- Base case
((k : Nat) -> prop k -> prop (S k)) -> -- Inductive step
(x : Nat) -> -- Show for all x
prop x
nat_induction prop p_Z p_S Z = p_Z
nat_induction prop p_Z p_S (S k) = p_S k (nat_induction prop p_Z p_S k) |
That is, for all properties on natural numbers, if it holds for zero and P n implies P (S n) then the property holds for all numbers. (proof by induction).
Table
in extensional type theory:
W-Type |
|||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
W-formation rule |
|
||||||||||||||
W-introduction rulewhere W means (W a : A)B(a) |
|
||||||||||||||
W-elimination ruleUsually a way to prove properties of W |
|
||||||||||||||
W-computation rule |
|
||||||||||||||
Intensional and Extensional TypeTheories
Intensional and Extensional TypeTheories are discussed on page here. One destinction is:
- In Martin-Löf extensional type theory two types are the same only if they are defined in exactly the same way.
- In Martin-Löf intentional type theory two types are the same if they are defined in the same way or if there is a proof that they are equal.
In category theory the locally closed Cartesian category is the counterpart of extensional type theory. For intensional type theory we need to add quotient completions - used for modeling extensional type theories into intensional ones. |
 |
Setoid
Setoids are discussed on this page.
The notion of setoid allows the intensional type theory to represent extensional concepts. Setoids provide a model of extensional type theory within the intensional one
In mathematics, a setoid (X, ~) is a set (or type) X equipped with an equivalence relation ~.
Often in mathematics, when one defines an equivalence relation on a set, one immediately forms the quotient set (turning equivalence into equality). In contrast, setoids may be used when a difference between identity and equivalence must be maintained, often with an interpretation of intensional equality (the equality on the original set) and extensional equality (the equivalence relation, or the equality on the quotient set). - From Wiki
One way to define a setoid is define a tuple consisting of:
- A type T (the carrier set).
- A relation ~.
- A proof that ~ is an equivalence relation over T
- the reflexivity a ~ a.
- the symmetry a ~ b if and only if b ~ a.
- the transitivity if a ~ b and b ~ c, then a ~ c.
For an Idris implementation of setoids see this github site
Extensionality of functions
if f(x) = g(x) for all x
then f = g
Example - consider the two functions f and g mapping from and to natural numbers, defined as follows:
- To find f(x), first add 5 to x, then multiply by 2.
- To find g(x), first multiply x by 2, then add 10.
These functions are extensionally equal; given the same input, both functions always produce the same value. But the definitions of the functions are not equal, and in that intensional sense the functions are not the same.
Functions between Setoids
Extensional Functions between SetoidsA function between setoids is a function between the underlying types (sets) together with a proof of extensionality: A function |f| : |X|->|Y| is extensional, with respect to the equalities of X and Y,if there is a term of type: f ~X=>Y g: Π|x|,|x'|:|X| x ~X x' -> |f|(x) ~Y |f|(y) The bars, as in |x|, indicate x is an element of the underlying type. This distinction will usually be dropped if extensionality applies. |
 |
Algebra of Extensional Trees
Topological Space and W-types
Are the structures of topological Spaces (especially Alexandrov topology) and W-types related in some way?
They both seem to be able to code linear structures and trees but not loops (circles).
Category Theory and W-types
In category theory W-types are initial algebras for polynomial endofunctors.
Doctrine
a categorification of the concept of “theory”.
Concepts
See:
- Quotient completion for the foundation of constructive mathematics - pdf
- W-types in setoids - pdf
- Elementry Doctrine (Lawvere) - pdf
- Split Fibration.
- Constructive Mathematics
- extensionality of functions
For more information about the relationship between type theory and category theory see this page.