Maths - Shapes

Here are some ways of modeling various Shapes:

	Homotopy Type	As Cell Complex
Circle
n-sphere
Torus
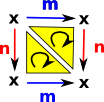Möbius Band
Projective Space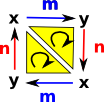
kleinBottle

For more information about constructing shapes as cell complexes see the page here.

N-Sphere

Here is more detail about constructing the n-sphere using paths.

0-sphere	1-sphere	2-sphere	3-sphere
			and so on...
The 0-sphere consists of 2 points. There is no non-trivial structure for higher dimensions.	The circle (1-sphere) consists of: 2 points. and 2 lines between these points. There is no non-trivial structure for 3D and above.	The hollow sphere (2-sphere) consists of: 2 points. 2 lines between these points. and 2 planes between these lines. There is no non-trivial structure for 3D and above.

Could the circle be constructed using just one base point and one line?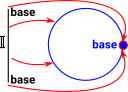

Contractibility of Singletons

see page here.

 

EuclideanSpace

home

Where Are You

This is one of a series of pages about topology, these pages start here.

For other pages, on the site, about topology see:

• Open Sets
• Fibre bundles
• Simplectical Complexes
• Delta Complexes
• Homotopy
• Homology
• Cubical Type Theory

See also:

• mathematical structures as simplical complex.
• shapes as types page.

Sheaves and Category Theory

• Topoi.
• Presheaves
• Category of Presheaves
• Cubical Type Theory

Computer Code Implementation

I have written some code to implement algebraic topology structures. For an explanation of this code see the page here.

Prerequisites

• Topology
• Set theory explained on this page.