Maths - Category Theory Universal Contructs Product

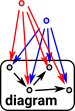
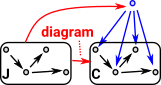
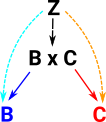
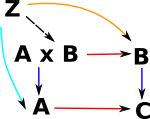
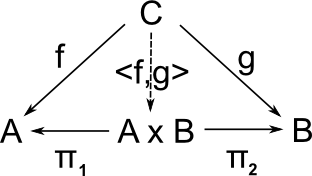
The (Cartesian) product of B and C is denoted B×C and is defined using this diagram which has arrows B×C -> B and B×C -> C .

Z represents any alternative candidate for a product, this must factor through B×C as defined by a universal property:

For every object Z and every pair of arrows Z -> B and Z -> C there must be a unique arrow Z -> B×C such that the diagram comutes.

Example in Set

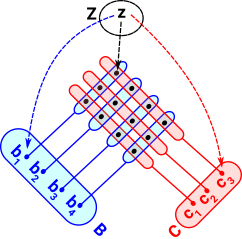In set, for every element which can be reached in B and every element which can be reached in C, there must be a unique element in B×C.

This two dimensional array corresponds to how we normally think of a Cartesian product.

The elements of the product can be represented as an array of ordered pairs like this:

{b₁,b₂,b₃,b₄}*{c₁,c₂,c₃}=

{{b₁,c₁},{b₂,c₁},{b₃,c₁},{b₄,c₁},
{b₁,c₂},{b₂,c₂},{b₃,c₂},{b₄,c₂},
{b₁,c₃},{b₂,c₃},{b₃,c₃},{b₄,c₃}}

So why can't we represent the set product in simpler ways like this:

In this case we could choose maps from Z->B and Z->C where the diagram does not commute.

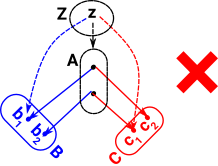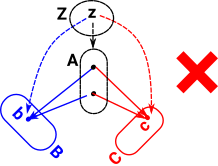Or if we have simpler surjective maps A->B and A->C on this diagram.

Then the map Z->A is not unique.

Also if we have injective maps A->B and A->C then the diagram may not commute.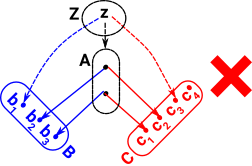

Products and Intersection

The above case suggests that, in the most general case, injective maps don't work for the projections. However, if we impose a limitation by making the product a pullback, then it works and the 'product' can represent an intersection.

see ncatlab

Products, Indexing and Inverse Projections

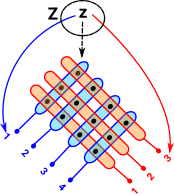Elements in the product can be identified by treating A and B as indexes (provided that we can invert the projections from the product).

To identify any element we need both projections.

Products in other Objects

In sets the product contains an array of ordered pairs, in more general objects these may not all exist.

For product topological spaces, products are taken at the level of the underlying sets and endowing them with an initial lift structure, the smallest or initial topology for which the projection maps are continuous. see ncatlab

A partially ordered set can be treated as a category, using the order relation as the morphisms. In this case the products and coproducts correspond to greatest lower bounds (meets) and least upper bounds (joins). see wiki.

Catagorical Products in Directed Graphs

Following on from the concept of catagorical product (discussed on page here) here we have an example where we have the product of two directed graphs.

In this example the objects to be multiplied together (B and C) both consist of two points and a directed line segment between them. The product will be a plane surface defined by the arrows shown here and their compositions.

To see this in more detail see the example of products in a simplicial set on this page.

In a Cartesian product there is an arrow from (g,h) to (g',h') iff:

there is a arrow from g to g'
or there is a arrow from h to h'

Concentrating on the connection between the product and C.

There is a map from the points in the product to the points in C (shown as red arrows).
We can construct an arrow, in the opposite direction, from the arrows in the product to the arrows in C (shown as blue double-line arrow).

So the structure in C 'lifts' up to the same structure between sub-graphs.

This is a similar construct to a fibration (see page here) but here we have not invoked the concepts of a topological space or continuous maps between them.

Table of Results

		Product (pullback)

generalisation		a kind of limit
set example		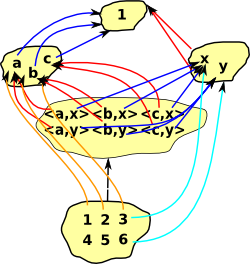Cartesian product {a,b,c}*{x,y}= {{a,x},{b,x},{c,x},{a,y},{b,y},{c,y}}
group		the product is given by the cartesian product with multiplication defined componentwise.
Grp (abelian)		direct sum
vector space		direct sum
poset		greatest lower bound meet
base topological space
POS		greatest lower bounds (meets)
Rng
Top		the space whose underlying set is the cartesian product and which carries the product topology
Grf
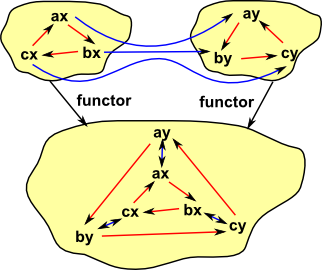
category		objects: (a,b) morphism: (a,b)->(a',b')

tensor products are not categorial products.

In the category of pointed spaces, fundamental in homotopy theory, the coproduct is the wedge sum (which amounts to joining a collection of spaces with base points at a common base point).