Representation Theory for Simplicial Sets
see wiki.
The Yoneda Embedding (see page here)
| Assume a category C where the objects are sets of points and the morphisms are total functions. | 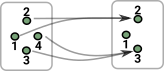 |
allows us to represent categories in set.
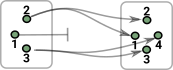 |
The opposite category to this Cop has the same objects but the morphisms are opposite which means elements in the domain may map to zero or multiple elements in the codomain. This corresponds to face maps and degeneracy maps in simplicial sets. |
| Adding an additional point (origin) allows each point to be represented as a vector. Then the morphism is represented by a matrix. |  |
More about representation theory for simplicial sets on page here.
| Can we use a category theory representable functor, that is an object with a homset to every other object? Would that give a vector space as above? |  |
Cayley's theorem
A simpler situation is representations of finite groups.
Cayley's theorem - every group G is isomorphic to a permutation group of the permutations of the underlying set.
| As an example here is a simple cyclic group defined by a Cayley graph. What permutation group is it isomorphic to? |  |
See page about Homotopy Groups for algorithm to convert Cayley graph to group.
Groupoids
If permutations are conditional, for example quantifier in predicate logic, see groupoid page.
