We can think of subobjects as a generalisation of subsets. (More about sets on this page).
On this page we look at the situation where part of a given mathematical structure is also an element of that structure. This is related to fixpoints as discussed on the page here.
These situations link together algebraic structures, logic and topology as discussed on the topos theory page.
Subset
 |
The concept of a subset is reasonably intuitive. Any set within the whole set, for instance, the elements with the yellow background on the diagram on the left. |
The concept of subsets creates lots of interesting structures, for instance,
Powersets
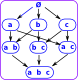 |
The set of all subsets shows that there is a lot of structure involved with subsets. |
Partitioned Sets
Here we don't just find a subset of set 'A' but we divide it completely into subsets. This is a set of sets. Non-overlapping sets, like this, are called a disjoint union.
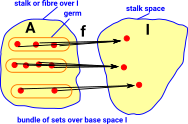 |
A partitioned set 'A' can be indexed over set 'I'. This is related to topology as described on page here. |
We can partition a set by using an equivalence class, all those elements that are equivalent form a subset.
Partitioning a set is a form of quotient, that is, we are dividing it into subsets. We use the notation A/~ where ~ is the equivalence relation. (See page here for groups).
Logic and Venn Diagrams
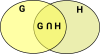 |
We can create new sets from the union and intersection of existing sets. We can relate this to 'and' and 'or' logic by using a 'predicate' function which returns true if an element is in a subset and false if its not. |
Notation
A![]() B means A is a subset of B
B means A is a subset of B
A![]() B iff
B iff![]() x
x![]() A :
x
A :
x![]() B
B
The![]() relation is:
relation is:
- Transitive: A
 B,B
B,B C->A
C->A C
C - Reflexive: A
 A
A
Sub-graph
We have looked at some concepts related to subsets, we now look at other structures and how can we subdivide these structures, also how the above concepts translate to them. We start with graphs in the sense of graph theory.
A subgraph is a graph 'G' is a graph where:
- The nodes are a subset of the nodes in 'G',
- The edges are a subset of the edges in 'G',
- The edges only connect to the nodes in the subgraph.
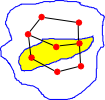 |
Given an arbitrary graph, how do we divide it into subgraphs? The nodes are easy enough, we could choose any subset of nodes, but what about the edges? If we choose an arbitrary set of nodes then, there will be some edges completely outside the subgraph, there will be some edges completely inside the subgraph and there will be some edges that cross over the border. |
Logic of a Graph
Above we saw how the concept of subsets is related to boolean logic. It turns out that subobjects of other structures are also related to logic, but it is a different logic for each structure. These other logics don't necessarily have just two values 'true' and 'false' but may have additional values. In the above graph example, we not only have a value representing the nodes being 'in' or 'out' of the subgroup, we also have values to represent whether the edges are 'in', 'out' or crossing the boundary.
This topic is discussed in more detail on this page.
Partition of a Graph
We can partition the nodes but, if the graph is connected, then we have the problem of edges that cross the boundary.
If we accept that edges are allowed cross the partitions then it is still useful to partition graphs in this way. Finding a graph partition with given properties is a NP-hard problem.
Sub-group
We can take a subset of the elements of a group, however its only a subgroup if it obeys the axioms of a group.
|
For instance, if we take the Cayley table on the left, the sub table with the yellow background also obeys the axioms for a group. So this is a subgroup. |
||||||||||||||||||||||||||||||||||||
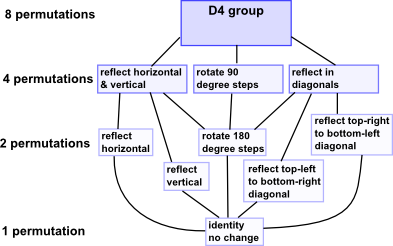 |
The subgroup structure can be represented by a Hasse diagram. This subgroup structure forms a lattice. |
Logic of a Group
Is there a logic associated with a group? According to Wikipedia, It is possible to encode an algebraic theory, as a topos, in the form of a classifying topos. The individual models of the theory then correspond to functors from the encoding topos to the category of sets that respect the topos structure.
Partition of a Group
Left or Right cosets of a subgroup partition a group. See page here.
let:
- H be a subgroup of group G.
- ~ be an equivalence relation on G
- a ~ b ↔ (ab−1
 H).
H).
The equivalence classes of ~ (the orbits of the action of H on G) are the right cosets of H in G. Or the left cosets if we swap a and b.
See page here for more about equivalences.
Equivalence
See page here.
Topos Theory
See page here.


