Cayley's Theorem
Cayley's theorem states that every group G is isomorphic to permutation group.
Where a permutation group is a subgroup of a symmetric group, that is a group whose elements are all the bijections from the set to itself, and whose group operation is the composition of functions.
 |
On the left of this diagram is an illustration of a permutation group. On the right is an illustration of a group as a binary operation and an inverse over a set. There is a 1:1 correspondence between each permutation and the set on the right. |
For pages related to Cayley's Theorem see the following:
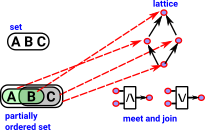
Example Cyclic Group
Here we want to relate permutations to other definitions of groups.
| So here we have a simple group, for example, in this case a cyclic group shown as a Cayley diagram: |  |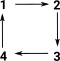
| A common method when we want to understand a structure is to look at functions between the structures. In particular 'functors' which are functions which preserve structure. |  |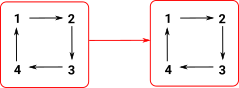
| Here we apply one element of the group, in this case '2', known as a representable. This must 'play well' with the internal structure of the group. |  |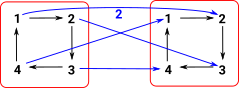
| If we repeat this for all permutations we get a set of permutations (homset). |  |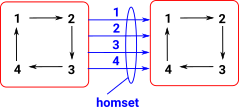
Other Representations
The group was represented by a Cayley diagram, in the example above, just to illustrate the situation graphically. Here we do the same example in terms of the group 'multiplication' operation.
| So lets take '2' as a representable then we can see that left 'multiplying' everything by 2 permutes the elements: |  |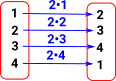
| Again if we repeat this for all permutations we get a set of permutations (homset). |
Further Information
For more information about functors see this page.
Cayley's Theorem is a special case of the Yonada Lemma (see this page). This extends this idea to other structures. So any structure can be represented as a functor into set provided it is representable.
