Notation for Permutations
Here we look at ways to represent permutations (although I will avoid describing them as 'representations' as that word has a more specific meaning for groups).
Diagram
The type of diagram on the left is the most intuitive. This clearly shows what inputs on the left are mapped to outputs on the right. We can easily combine several permutations together by putting several of these together. Note: if the arrows go from left to right, as here, then we need to reverse the order from the order of operands in an equation. |
Permutation Vector
|
For each index we can see the value it maps to. | ||||||
|
Or if we don't want to use indexes then we can use two rows to show the 'to' and 'from' values. |
Permutation Matrix
|
The permutation matrix uses the indices in the vertical and horizontal dimensions to represent the input and outputs. We can then use 1 if the input and output are connected and 0 if it is not. This is not a very concise representation but it has the advantage that matrix multiplication represents concatenation of permutations. |
Cycle Notation
| (1 2 3) | loops are indicated by brackets. |
Discussion
The permutation group seems to me to have a sort of indirection about it. We start with a set, we define some permutations of the set, we then treat these permutations as another set and this set of permutations are the elements of the group.
So a permutation group is defined as group G whose elements are permutations of a given set M and whose group operation is the composition of permutations in G.
A permutation (in this context - it is defined differently from the way the term is used in probability which involves the linear order) is a 1:1 mapping from a group to itself. that is each element of the set maps to one other (or possibly the same) element of that set. In technical terms: this is a bijection from a finite set to itself.
Example 1
| e
= (1)(2)(3)(4) a = (1 2)(3)(4) b = (1)(2)(3 4) a o b = (1 2)(3 4) |
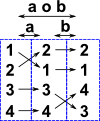 |
Example 2 - Triangle

In this example lets take the rotation of an equilateral triangle to itself. This has 3 possible rotations:
| identity (0°) | anticlockwise (120°) | clockwise (240°) | |
| permutation | |||
| cycle notation | (1)(2)(3) | (1 2 3) | (3 2 1) |
These letters then become the elements of a set of permutations. We can then work out the result of the composition of these permutations:
o |
= |
To be consistent with other literature on this, we need to reverse the order of the functions, that is the right hand function is applied first then the left hand function. That is:
(d o c)(x) = d(c(x))
where:
- d(x) = apply the 'd' permutation to x
- c(x) = apply the 'c' permutation to x
- o = composition operation
- (d o c)(x) = apply the composition of c then d to x
We can draw up a complete table of the composition operation which defines this example completely:
| row o col | i | c | d |
|---|---|---|---|
| i | |||
| c | |||
| d |
We can also work out the inverse of each permutation:
| x | |||
|---|---|---|---|
| x-1 |
We can extend this group to include reflections, see this page for more.
Example 3 - Cube
Lets take as an example the rotation of a cube in ways that does not change its shape (i.e. multiples of 90° rotations about x, y or z) although we will keep track of the rotations possibly by markings on the faces of the cube. see this page.
