Maths - Size (Order) of Groups

Here we will categorise how many and what type of groups there are of a given size (known as 'order' in the terminology. There is at least one group of a given size, that is the cyclic group, for instance if we are looking for a group of order 'n' then C_n is such a group. There may, or may not, be other groups of order n.

Order 1

Every  group must contain the identity element so since the group only contains one element this must be the identity element.

Order 2

There is only one valid group of order 2, all other groups of order 2 are isomorpic to this.

Cayley Graph	Table
	e m e e m m m e

This is often called C₂, the cyclic group of order two. Equivilantly it is also Z₂, the group of integers modulo two.

Order 3

Cayley Graph	Table
	e r r² e e r r² r r r² e r² r² e r

There is also only one group of order 3 this is C₃.

Order 4

Cayley Graph	Table	Table (isomorphism)
	e r r² r³ e e r r² r³ r r r² r³ e r² r² r³ e r r³ r³ e r r²	e r² r r³ e e r² r r³ r² r² e r³ r r r r³ r² e r³ r³ r e r²
	e v h vh e e v h vh v v e vh h h h vh e v vh vh h v e	e r² r r³ e e r² r r³ r² r² e r³ r r r r³ e r² r³ r³ r r² e

There are two possible groups of order 4:

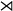• C₄ = C₂C₂
• V₄ = C₂×C₂

Order 5

Order 6

 

 

EuclideanSpace

home

Set Definition

Function Definition

1:1 Correspondence Definition