So far, we have defined a group as a set+structure, here we want to use the same structure but on top of other types of categories, so instead of defining a group in terms of its internal elements we define it in terms of its external properties, that is structure preserving mappings called functors (this is the category theory approach see this page).
To do this we take the structure in terms in the group identities:
- Associatively: (a b) c = a (b c)
- Identity element 'e' such that: e a = a = a e
- Inverse element 'a-1' such that: a a-1 = e = a-1 a
and we put this in category theory terms:
We define:
- a multipication mapping: μ: G×G -> G
- an inverse mapping: i: G -> G
- a identity mapping: e: * -> G
and now define the identities in these terms:
| Group Associativity | μ(a,μ(b,c)) = μ(μ(a,b),c) μ(id×μ)(a,b,c) = μ(μ×id)(a,b,c) μ(id×μ) = μ(μ×id) |
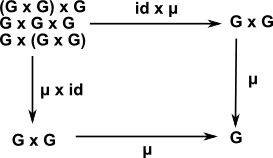 |
| Group Identity | μ(a,a-1) = e | 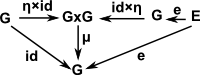 |
| Group Inverse | 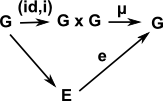 |
