In a finite group there are discreet or finite steps between elements of the group. We cannot move continuously between them as we can in infinite groups.
Permutation group
The permutation group seems to me to have a sort of indirection about it. We start with a set, we define some permutations of the set, we then treat these permutations as another set and this set of permutations are the elements of the group.
So a permutation group is defined as group G whose elements are permutations of a given set M and whose group operation is the composition of permutations in G.
A permutation (in this context - it is defined differently from the way the term is used in probability which involves the linear order) is a 1:1 mapping from a group to itself. that is each element of the set maps to one other (or possibly the same) element of that set. In technical terms: this is a bijection from a finite set to itself.
Cayley's Theorem
Every group can be interpreted as a permutation group.
Cycle Decomposition
We could define each permutation by how it maps each element such as:
a
-> b
b
-> c
c
-> d
d
-> a
and so on. However we could save space by combining them on a single line as follows:
a -> b -> c -> d -> a
This is quite a simple case where all the elements cycle round. The opposite extreme to this would be the null element where each item stays the same:
a
-> a
b
-> b
c
-> c
d
-> d
In the more general case there may be a number of cycles. such as :
a
-> b -> a
c
-> d -> c
There is a notation that allows us to write this even more compactly. The above case could be written:
(ab)(cd)
That is, each cycle is shown in a separate set of brackets.
Group Elements
Each of the permutations is an element in the group. It is almost like indirection in that we can define each permutation then we can define how they interact under composition.
Example 1
| e
= (1)(2)(3)(4) a = (1 2)(3)(4) b = (1)(2)(3 4) a o b = (1 2)(3 4) |
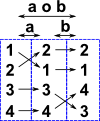 |
Example 2 - Triangle

In this example lets take the rotation of an equilateral triangle to itself. This has 3 possible rotations:
| identity (0°) | anticlockwise (120°) | clockwise (240°) | |
| permutation | |||
| cycle notation | (1)(2)(3) | (1 2 3) | (3 2 1) |
These letters then become the elements of a set of permutations. We can then work out the result of the composition of these permutations:
o |
= |
To be consistent with other literature on this, we need to reverse the order of the functions, that is the right hand function is applied first then the left hand function. That is:
(d o c)(x) = d(c(x))
where:
- d(x) = apply the 'd' permutation to x
- c(x) = apply the 'c' permutation to x
- o = composition operation
- (d o c)(x) = apply the composition of c then d to x
We can draw up a complete table of the composition operation which defines this example completely:
| row o col | i | c | d |
|---|---|---|---|
| i | |||
| c | |||
| d |
We can also work out the inverse of each permutation:
| x | |||
|---|---|---|---|
| x-1 |
We can extend this group to include reflections, see this page for more.
Example 3 - Cube
Lets take as an example the rotation of a cube in ways that does not change its shape (i.e. multiples of 90° rotations about x, y or z) although we will keep track of the rotations possibly by markings on the faces of the cube. see this page.
Symmetric group
The group of all permutations is the symmetric group. The term permutation group is usually used for a subgroup of the symmetric group.
The number of possible ways to order the set is n factorial as we can see from this table:
| number of elements of a set | possible ways to order set |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| n | !n |
There is a 1:1 correspondence between the ordering of the set and mappings between the set and itself. For instance, in the table below, under reordering we show the elements of the set being rearranged and under mapping we show each element being mapped to another element:
| Reordering | Mapping |
|---|---|
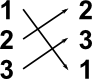 |
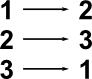 |
But these are both ways of denoting the same set, i.e. each element of the set maps to another (or possibly same) element of the set.
We can assign a letter to each of these mappings:
| permutation | ||||||
|---|---|---|---|---|---|---|
| cycle notation | (1)(2)(3) | (1)(2 3) | (1 2)(3) | (1 2 3) | (3 2 1) | (1 3)(2) |
These letters then become the elements of a set of permutations. We can then work out the result of the composition of these permutations:
o |
= |
To be consistent with other literature on this, we need to reverse the order of the functions, that is the right hand function is applied first then the left hand function.
We can draw up a complete table of the composition operation which defines this example completely:
| row o col | i | a | b | c | d | e |
|---|---|---|---|---|---|---|
| i | ||||||
| a | ||||||
| b | ||||||
| c | ||||||
| d | ||||||
| e |
We can also work out the inverse of each permutation:
| x | ||||||
|---|---|---|---|---|---|---|
| x-1 |
Conjugacy Classes
Any group H splits up into subsets C with the following properties.
-
Each subset C is obtained in the following way: you take any group element, say x. Then you take all of the elements of the group, call them g's and form the group products g o x o g-1. Notice that x itself is one of these products, because e o x o e-1= x. The subset that consists of all these g o x o g-1's is one of the C's. For example, x is an element of the C that you get by starting with x. It does not matter which x in C you start with. You get the same bunch of elements, namely C.
-
Any two elements of C have the same character value under every representation r. In symbols: if x and y are in the same C, then x(x)=x(y).
These subsets C are called the 'conjugacy classes of H' The C's are often quite large. The larger they are, the more the group law of H fails to be commutative.
