We have already looked at groups and on these pages we look at other algebraic structures.
For a more general discussion of algebras see the page here.
F-Algebras
 |
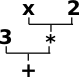An algebra consists of:
|
If the datatype is denoted 'A' then going one layer up in this tree structure can be denoted: F(A).
So to evaluate an expression we need a function α: F(A) -> A
More about f-algebra here.
Computing with Algebras
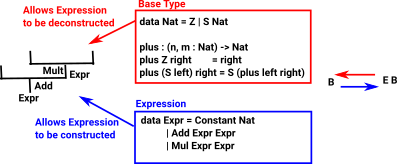
If we have a 'base type' such as Nat we can construct an algebra from that. So 'Expr' builds up a tree structure and the base type allows us to contract it down again.
We can expand Expr to include variables like this: In this case we can't always reduce the expression to a single value. In many cases we would use de Bruijn notation rather than naming the variable with a string. |
data Expr = Constant Nat
| Var String
| Add Expr Expr
| Mul Expr Expr |
Fixpoints of Expression
An expression is defined recursively so an expression can exist inside an expression and so on. Otherwise we could have say 1+6 but not 1 + (2 * 3).
So an expression of an expression is still an expression, that is:
Expr X = Expr (Expr X)
This is called a fixed point often contracted to fixpoint.
Existence of Fixpoints - Monotonicity
A fixpoint is guaranteed to exist if the function is monotone (Knaster-Tarski fixpoint theorem).
That is, if there is an order on the elements and the function preserves the order.
This applies even if the order is a partial order provided there is a bottom element.
This order may be thought of in different ways depending if we are coming from the direction of denotional semantics or category theory:
| Denotional Semantics | Category Theory | |
|---|---|---|
| More information | ||
| Order | Lower means less well defined and higher means more defined. | Lower means toward 'initial' and higher means toward 'final'. |
| Bottom Element | Denoted  . This means undefined/error/non-terminating computation. |
The least fixed point is the fixed point with a morphism to every other morphism. |
The semantics should not just be monotone but also continuous , in which the least fixpoint is the union of all finite iterates.
Functions for which f() = are called strict.
Strictly Positive Functor
An inductive type is defined by a functor but not all functors can be used to define an inductive type.
A functor is strictly positive if it is defined by an expression that only uses constant types, the variable type X and the operators ×, +, ->, so that X only occurs to the right of arrows. Arrows (functions) are covarient in codomain and contravarient in domain.
More info on this site and this site.
