Galois Theory concerns the solution of polynomial equations.
The Galois group G is a permutation group. Its elements are permutations of the solutions of polynomial equations that preserve addition and multiplication.
Number Systems and Field Extensions
| Number System | Includes: | Solution to equation with operations: |
|---|---|---|
| N - natural numbers | numbers used for counting:1,2,3 | +,* |
| Z - integers | includes zero and negative numbers | +,*,- |
| Q - rational numbers | which can be represented by one integer divided by another | Linear: +- × ÷ |
| Qalg - algebraic numbers | includes roots with any arithmetic (+- × ÷) operations | polynomial upto degree 4 : +- × ÷ (may require √-1) |
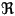 - real numbers - real numbers |
includes everything on a continous geometric line including transcendentals like π. | all polynomials (may require √-1) |
| C - complex numbers | includes imaginary numbers √-1 | all polynomials |
- Note 1: symbols for number systems are usually shown as a gothic looking font with a double image but I can't find a sutable font for use on the web.
- Note 2: more about number systems on this page.
These number systems form a hierarchy starting with natural numbers, used for everyday counting, then moving on to fill in more gaps in the number line and represent the solutions to more complicated equations. We might think of each type forming an extension to the last so we only need to choose the minimum number system that has the solution to the type of equation that we are trying to solve.
If we are solving a polynomial which can be factorised then we only need Q (Rational numbers).
If a polynomial can be solved by a formula then it must be an algebraic number or less complicated (higher in the above table) in other words, if the solution is say a transcendental, then there won't be a formula for it because a finite formula can't produce a transcendental number.
Therefore, deciding if a polynomial is solvable by formula, is equivalent to finding out whether the solutions are all algebraic numbers.
Properties of Galois Group
G is an infinite group but the values for a specific polynomial form a finite subgroup. G is a symmetry because it preserves + and *.
If g is an element of G, a permutation (function) from Qalg to Qalg.
- g is a function which maps Qalg to Qalg
- g(root of polynomial) = another root of same polynomial (if f(p)=0 then f(g(p))=0)
- g(p + q) = g(p) + g(q)
- g(p - q) = g(p) - g(q)
- g(p * q) = g(p) * g(q)
- g(p / q) = g(p) / g(q) if q ≠ 0
- f(g(p)) = g( f(p)) for any functction f
- if p ≠ q then g(p) ≠ g(q)
- g(0) = 0 since g(p - p) = g(p) - g(p)
- g(1) = 1 since g(p / p) = g(p) / g(p)
- g(2) = 2 since g(1 + 1) = g(1) + g(1)
- g(m/n) = m/n where m & n are integers (by induction from above)
- g(m + i n) = m - i n (maps complex numbers to conjugate)
- g(√2) = -√2
- g(√3) = √3
Galois Connection
Galois theory makes a connection between two lattice structures (lattices are described on this page). These lattices are structures where each element is itself an algebra.
| Subgroups | Subfields Field Extension to Q |
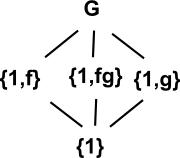 |
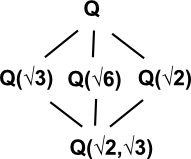 |
