Dihedral Group D3
In this example lets take the mapping of the equilateral triangle to itself, that we looked at in the introduction, but this time we will also include reflections. So we end up with the identity, 2 possible rotations and 3 possible reflections. This is all the possible permutations so this is a symmetry group:
| identity (0°) | anticlockwise (120°) | clockwise (240°) | |
| permutation |  |
 |
 |
| cycle notation | (1)(2)(3) | (1 2 3) | (3 2 1) |
| reflect in 1 - 23 | reflect in 2 - 13 | reflect in 3 -12 | |
| permutation |  |
 |
 |
| cycle notation | (1)(2 3) | (2)(1 3) | (3)(1 2) |
So, what is the minimum set of generators to generate this group?
We can generate the rotations by combining two reflections:
 |
= |  |
 |
= |  |
 |
 |
= |  |
 |
= |  |
 |
So the 3 reflections will generate the group, but we don't need 3 because once we have one rotation we can generate the other reflection.
So 2 permutations are needed to generate the whole group, we can either use:
- 2 different reflections, or
- 1 reflection and 1 rotation
however we can't use 2 rotations because rotations form a self contained subset of this group.
So, as an example, lets choose the generators to be 'a' and 'b' where:
- a = ma reflection through in 1 - 23
- b = ma reflection through in 2 - 13
We can generate all the permutations as follows:
- e = 1
- ma = a
- mb = b
- mc = aba
- ra = ba
- rb = ab
Cayley Table
The complete table is:
| 1 | a | b | aba | ba | ab | |
| 1 |  |
 |
 |
 |
 |
 |
| a |  |
 |
 |
 |
 |
 |
| b |  |
 |
 |
 |
 |
 |
| aba |  |
 |
 |
 |
 |
 |
| ba |  |
 |
 |
 |
 |
 |
| ab |  |
 |
 |
 |
 |
 |
or we can show this completely in terms of the generators:
| 1 | a | b | aba | ba | ab | |
| 1 | 1 | a | b | aba | ba | ab |
| a | a | 1 | ab | ba | aba | b |
| b | b | ba | 1 | ab | a | aba |
| aba | aba | ab | ba | 1 | b | a |
| ba | ba | b | aba | a | ab | 1 |
| ab | ab | aba | a | b | 1 | ba |
Ways to define the structure of this group
What is the minimum information required to define the structure of this group? We could:
- Specify each permutation in the group by using the 3 arrows as shown above for each permutation.
- Specify each permutation in the group by using the cycle notation for each permutation.
- By the Cayley table for the group.
Another way to define the group is the 'Presentation of the group', as explained on this page, for this example it is:
Γ< a,b | aa,bb,bab=aba>
We could have set all relations to be equal to unity by replacing bab=aba with baba-1b-1a-1=1
Can we use this to generate all the entries in the table and thus competely define the structure?
Lets take an example of multiplying 'ab' by 'ab':
ab * ab = abab [associativity]
= aaba [since bab=aba]
= ba [since aa=1]
Doing this for all the other entries in the Cayley table shows that this competely defines the group. How can we work out the minimum set of relations that will define the group?
Cayley Graph
Upto now we have chosen to use two reflections for the generators but it is more common to use 1 rotation and 1 reflection because can be more easily generalised to an 'n' sided dihedral. This is given by one cycle going clockwise and another going anticlockwise connected by the reflections.
Here are Cayley graphs for the case where the generator is 1 rotation + 1 reflection and the case where the generator is 2 reflections.
| Generator | 2 reflections | 1 rotation + 1 reflection |
|---|---|---|
| Presentation | < a,b | aa,bb,bab=aba> | < a,b | aa,bbb,a-1ba=b-1> |
| Graph | 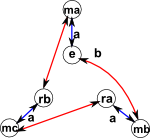 |
 |
Given two Cayley graphs can we find if they represent the same group?
Sandwich Product
The form y x y-1 has some interesting effects:
For instance if y is a rotation and x is a reflection, then we get a different reflection
 |
 |
 |
= |  |
Or if x is a rotation and y is a reflection, then we get the inverse rotation.
 |
 |
 |
= |  |
So: m r m -1 = r -1
