One of the simplest and most fundamental dualities is the duality between points and lines in 2D space. Expressions that involve points and lines can be rewritten in a way that points and lines are interchanged, for instance:
- Two lines define (meet at) a point.
- Two points define (joint to make) a line.
In 3 dimensions the dualities change, in this case there is a duality between points and planes, in 'n' dimensions we can predict the dualities because they have a binomial structure. This is reflected in the structure of Geometric Algebra, as explained here, which makes Geometric Algebra useful when we want to transfer geometry and physics between a different number of dimensions.
It is not only in geometry and algebra that these dualities occur, many of the physics quantities have corresponding dualities, here are some examples:
| Field | First Dual | Second Dual | Example | Applies in | switch |
|---|---|---|---|---|---|
| tensors |
contravarient |
covariant |
any dimensions ? | gram matrix | |
| geometric algebra | vector |
directed area |
3 dimensions | multiply by pseudo-scalar | |
| calculus | differentiation | integration | electrostatic and magnetic fields | any dimensions | |
| calculus | normal space | tangent space | |||
| field theory | scalar field | vector field | electro-magnetic fields, kirchoff's law | 3 dimensions | diff or integrate |
| algebra | inner product (dot product) |
outer product | any dimensions 3 for cross product |
||
| algebra | a | 1/a | any dimensions | invert | |
| orthogonal matrix | rows | columns | orthogonal coordinates | transpose | |
| transform sandwich products | q P q-1 | q-1 P q | any dimensions | reverse transform | |
| geometry platonic solids |
dodecahedron |
icosahedron |
3 dimensions | swap faces and verticies. | |
From some points of view, for example when studying tensors, it almost seems like these dualitys are all the expression of the same correspondence. its as if we can put all the things in the 'first dual' column together and they form a consistent model of the world and then we can put all the things in the 'second dual' column together and they form a mirror image model of the original world.
However I have to restrain myself from taking it too far. There are lots of limits to this, for example some of these things only work in 3 dimensions (in 4 dimensions there may be a different set of dualities, for example vectors and trivectors). There may also be other constraints, some things may depend on orthogonal coordinates.
Perhaps the above model is too simplistic in that i have mixed together elements like scalar and vector fields together with operators which switch between them. It might be better to draw this in a two dimensional way like a morphism?
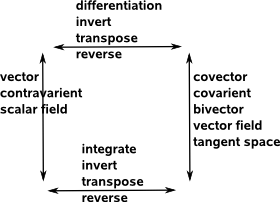
There are another set of dualities which I'm tempted to add to the above (perhaps that's taking things a bit too far, I don't know?):
| Field | First Dual | Second Dual | Example | Applies in | switch |
|---|---|---|---|---|---|
| logic | and gates | or gates | De Morgan duality | not gate | |
| probability | permutations | combinations | 1-prob | ||
| symmetry | right handed | left image | mirror image | mirror image | |
| parity | even | odd |
There are arguments that I could make to add these, for instance, both seem to have a mirror image property and the binomial triangle seems to be involved in both?
A lot more speculative but I get the impression that there is a duality between translational and rotational quantities, as suggested on this page, such as:
| Field | First Dual | Second Dual | Example | Applies in | switch |
|---|---|---|---|---|---|
| transforms | translation | rotation | |||
| coordinates | rectangular | polar | |||
| quantum mechanics | particles | waveform |
Vector, Covector and Bivector
Covectors come from tensor algebra whereas bivectors come from Clifford/geometric algebras however despite their different origins, if we restrict ourselves purely to 3 dimensional euclidean space, then the two ideas turn out to represent the same thing as explained on this page.
Contravarient and Covariant
When defining vectors we use the linear combination of basis vectors. Since the physical vector is fixed, then, if we change the basis vectors then the vector components will automatically change in the inverse way.
Scalar Field and Vector Field
I always thought that scalar and vector fields were completely different physical entities, for instance,
- scalar field - temperature at each point in space.
- vector field - force field caused by say gravity.
However we can always convert from one type to another type by differentiation and integration so, for example, temperature gradient would be a vector field.
The other duality is combining two vector fields by using the dot product to give a scalar field (or a vector fields with its dual by using the dot product to give a scalar field).
Tangent Space
In addition to the scalar and vector fields above we have a duality between the vector tangent and normal spaces.
Differentiation and Integration
Or the vector calculus such as:
- Div takes a vector field as an input and returns a scalar field
- Grad takes a scalar field as input and returns a vector field
- Line integrals involving dot product convert vector to scalar
Inner Product and Outer Product
- Inner product where one operand is a vector decreases grade.
- Outer product where one operand is a vector increases grade.
Rows and Columns
When using a matrix transform based on orthogonal coordinates then transposing the rows and columns inverts the transform.
Geometric Algebra Transforms
Transforms in geometric algebra are represented by sandwich products q P q-1 and q-1 P q which are inverses of each other. That is if we apply q P q-1 to a point and then apply q-1 P q to the result we get back to the original point.

