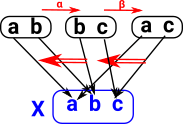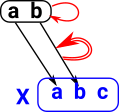Maths - Topoi

Topos theory describes set theory using category theory. It allows us to take some nice properties of sets and to generalise them to certain categories with the properties described below.

So far, when we have used category theoretical methods to look at sets, the objects have been the empty set, a one element set, a two element set and so on. Without any extra structure a two element set is isomorphic to any other two element set.

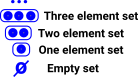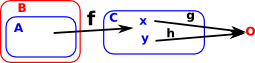
However, there is some other structure inherent in a set that we would like to look at in a category theoretical way (from the outside). This is the structure of the sub objects (such as subsets)

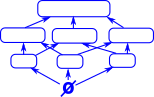
External Diagram The arrows here are inclusions indicating one set is a subset of another.

In order to relate this to the internal structure I have labeled the elements to try to get some intuition for the external diagram.

Internal Logic

see ncatlab

The basic ideas of the internal logic induced by a given category C are:

• the objects A of C are regarded as collections of things of a given type A
• the morphisms A->B of C are regarded as terms of type B containing a free variable of type A (i.e. in a context x:A)
• a subobject φA is regarded as a proposition (predicate): by thinking of it as the sub-collection of all those things of type A for which the statement φ is true
• the maximal subobject is hence the proposition that is always true; this is the logical object of truth TA
• the minimal subobject is hence the proposition that is always false; this is the logical object of falsityA
• one proposition implies another if as subobjects of A they are connected by a morphism in the poset of subobjects: φ=>ψ means φψ

Logical operations are implemented by universal constructions on subobjects.

• the conjunction and is the product of subobjects (their meet)
• the disjunction or is the coproduct of subobjects (their join)
• the existential quantifier is the support of the dependent sum of subobjects
• the universal quantifier is the dependent product of subobjects

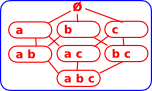
Finite Set Example

Although we think of finite sets as being something very simple which we can then add structure to, sets do have an inherent rich substructure of their own.

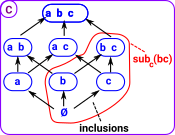
Take a set, say: X = {a,b,c}

From this we can generate all the subsets (power set) and we can generate arrows which are injective maps (inclusions) showing the subset relations.

There is another way to characterise subsets of X, that is a map from X to Bool (a set with two elements, true and false).

So each element in the powerset corresponds to a map: X->2.

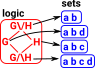
			category	logic
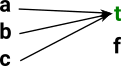	X={a,b,c}	For example X contains a, b and c so they all map to true.	terminal object	true (unconditional)
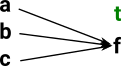	Ø = {}	The empty set Ø does not contain a, b and c so they all map to false.	initial object	false
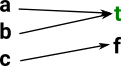	{a,b}	For any other subset, say {a,b}, the elements in the subset map to true and the others map to false.		true if a and b

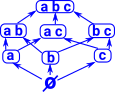
Internal Structure	External Structure
The blue boxes in this diagram are sets (objects in the set category) so {a,b} is a set with two elements a and b. The black arrows represent inclusions between these objects, that is, one set is included in another. So the diagram shows the substructure and consists of the power object with inclusion arrows between its elements. In this diagram there are 0 or 1 arrows between any two objects so this is a preorder. In particular it is a bounded lattice because it has a greatest lower bound and least upper bound. In category theory terms it has: all products all coproducts an initial object a terminal object. 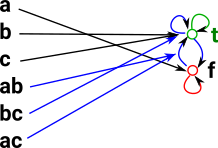As an algebra it is a Heyting algebra	In category theory we look at objects from the outside. That is the morphisms in and out of them. Here we use a truth object Ω described below. In this case (of sets) the truth object is a Boolean value denoted 2. It has two elements: true t and false f. All the morphisms to Ω are given by Hom(X,Ω).

I have tried to draw how the internal elements map but the diagram gets a bit messy. So I think its better to represent this homset as a table: b c f f f t t f t t

In Category Theory

An (elementary) topos is a category that:

• Is finitely complete
• Is finitely co-complete
• Has exponentiation
• Has a subobject classifier

This is equivalent to:

• being Cartesian closed
• and having a subobject classifier

Finite limits and co-limits means:

In category Theory	What this looks like in set
an initial object	empty set
a terminal object	an object like a set with one element
binary coproducts	disjoint union of two sets
binary products	Cartesian product of two sets
equalizers	subset of X consisting of all elements x such that f(x) = g(x), where f,g: X -> Y
coequalizers	quotient set of X where two elements f(y) and g(y) are identified, where f,g: Y -> X

see John Baez website for fuller explanation of this

Example Topos in Set

The main example of a topos is set, in other words an (elementary) topos is a set-like category.

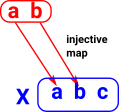
In order to understand sets we need to describe the structure of subsets. We need to define an element of the powerset. One way to do this is as follows:

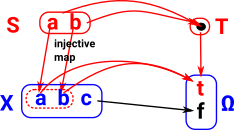
One way to define S as a subset of X (that is: SX) is to specify an inclusion (or injection map) from S to X. An injective function is one where no two distinct inputs give the same output.
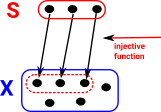It would not work to have a map in the other direction because elements in S are not uniquely identified with elements in X.
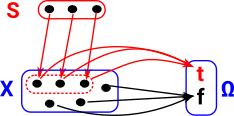
However we can define a subset with a map going out of X. This maps onto a two point set {f,t}. Those elements that are in the subset map to 1 and those that are not map to f. This is called the characteristic function. So in the case of set Ω is a 2 element set like Boolean algebra. The logic of a Topos is not necessarily Boolean logic, it is constructive (intuitionistic) logic as described on the page here. Its only the true elements that commute.
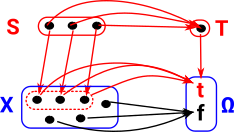
We can complete the diagram by mapping through the terminal object T (in this case the 1 element set). All elements in S map to it. The map T->Ω picks out the true elements of Ω. As we can see, the diagram commutes. Each injective map from the subsets corresponds to a map χ : X->Ω where χ is the Greek letter Chi.
The diagram relates the set category to the logic of boolean algebra but without the law of the excluded middle, that is intuitional or constructive logic.

Generalisation to Non-sets

We can generalise from elementary topos based on sets to other topoi.

We generalise this to categories that are not sets. X becomes some category and S becomes a sub-category. The injective mapping becomes a monic arrow. The characteristic function then becomes the sub-object classifier.

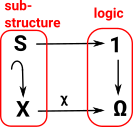The set example above then a Boolean type is the sub-object classifier, however, if we have additional structure, for example a graph, then the sub-object classifier becomes more complicated.

Example - Graph

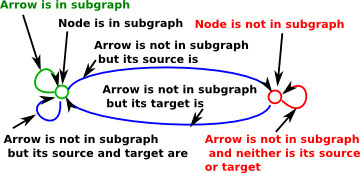
In the set example above Ω contains just true and false with the familiar Boolean logic. In the following more complicated examples there are also true and false corresponding to the cases where the subobject is completely in or completely out of the whole object. In addition there may now be other cases which are not but are required to allow the injection map to be valid. A good example of this is a graph category:

The terminal object for graph is one node with a loop.
The sub-object classifier for graph has two nodes and 5 arrows. For nodes: Is not in subgraph Is in subgraph For edges: Is in subgraph Not in subgraph but its source and target are. Not in subgraph but its source is. Not in subgraph but its target is. Not in subgraph and neither is its source or target.
The truth object.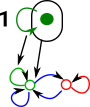
As with sets this is constructive (intuitionistic) logic as described on the page here.

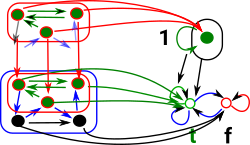Internal Structure	External Structure
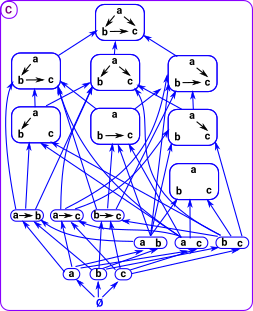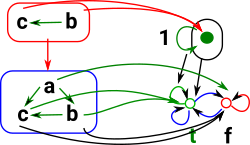
Here we look at the substructure of a graph, each of the blue boxes is a graph object. In this diagram the black arrows inside the boxes are the edges of the graph and the blue arrows outside are the inclusion arrows of the lattice. This is a lot more complex than the set example above because both the nodes and the edges and all combinations can change.	In category theory we look at objects from the outside. That is the morphisms in and out of them. Here we use a truth object Ω described above. All the morphisms to Ω are given by Hom(X,Ω).

I have tried to draw how the internal elements map but the diagram gets a bit messy. So I think its easier to represent like this.

How do we extend this beyond graphs to simplicial sets?

Alternative Viewpoint

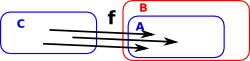
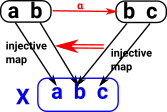
We have two sets, 'A' and 'B', with an arbitrary mapping 'F' between them. We can define a subset of set 'B' by using the predicate 'P'. For every subset of 'B' defined by 'P' there exists a subset of 'A' defined by 'R'.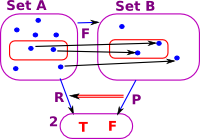
However this does not necessarily work in the other direction. Here is an example of a subset of 'A' which does not map to a subset of 'B'.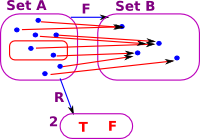

So the map 'F' between objects induces a contravarient map between arrows P->R.

See also Yoneda embedding.

Topos and Logic

A logic is defined over a type. So if we have a type, say 'set', then its sub-stucture will correspond to a logic as described below. A different type, say 'POSET', will have a different logic.

Logic of Set Example

Here we look at the logic of the set example (described on page here) and how this corresponds to the subset structure.

In this diagram we have multiple subsets of X. Each one will have its own injective map into X and also its own map into the truth object. To show all the arrows for all 3 subsets would make the diagram very complicated so I have just indicated where the arrows go for each subset. Each injective map from the subsets corresponds to a map χ : X->Ω where χ is the Greek letter Chi. so χA corresponds to the subspace A and so on.

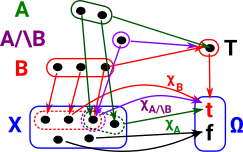We can split the χ map, first into ΩA×ΩB then map this to ΩA/\B. This second part corresponds to the Boolean 'and' function.

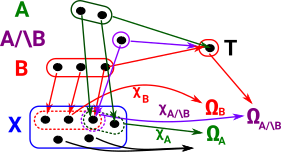In the diagrams below the dark green represents a subobject of the light green and the dark blue represents a subobject of the light blue. They can be combined in various ways:

and (meet)		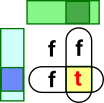/\(Ω,Ω) -> Ω	f t f f f t f t
or (join)		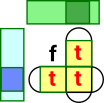\/(Ω,Ω) -> Ω	f t f f t t t t
implies		=>(Ω,Ω) -> Ω	f t f t t t f t

Logic of Graph Example

The logic of the nodes is the same as the set example:

and (meet)		/\(Ω,Ω) -> Ω	f t f f f t f t
or (join)		\/(Ω,Ω) -> Ω	f t f f t t t t
implies		=>(Ω,Ω) -> Ω	f t f t t t f t

but now we also have the edges, here is my attempt to construct a truth table for 'and':

	none	f->f	f->t	t->f	t->t
none	none
f->f		f->f	f->f	f->f	f->f
f->t		f->f	f->t	f->f	f->f
t->f		f->f	f->f	t->f	t->f
t->t		f->f	f->f	t->f	t->t

For instance, if an edge goes from true to true (t->t) in 'A' and it goes from true to true in 'B' then it must be in their intersection and therefore goes from true to true in 'A/\B'.

What if it goes from true to true (t->t) in 'A' but it goes from false to false in 'B' then it can't be in their intersection and therefore goes from false to false in 'A/\B'.

So it looks like we can 'and' the source and target separately to give the resulting edge.

Example - Dynamical Systems

The terminal object for dynamical systems is one node with a loop.
The sub-object classifier for dynamical systems. '0' represents 'true' all other numbers indicate how many steps before it becomes true.
The truth object. points to '0' representing true.
All nodes and edges in the subobject go to '0' which represents 'true' all other nodes goto the number which indicates how many steps before it becomes true.

Subobject Classifier

See page here for a non-categorical approach to sub-objects.

If the arrow 'f' is monic (injective) then it maps to a subobject (subset) of 'B'. That is: there is a subobject of B that is isomorphic to A.

The inclusion relation on subobjects is:

• reflexive
• transitive

In order to define the subobject we must define the monic 'upto equality' which is not in the spirit of category theory. We will go on to define a 'subobject classifier' which defines a subobject, in a much more category theoretic way, by the composition of maps (and also relates the whole subject to logic).

Naming Arrows

In category theory we don't usually identify elements, such as elements of a set, because we only tend to determine things 'upto isomorphism'. The objects in a category are whole 'structures', they don't represent individual elements.

However, there is the possibility to indicate elements indirectly using arrows. For instance, if we want to enter a specific element we can use:

1->A

because, in sets, 1 is the single element set so it will indicate an element uniquely.

We can also use naming arrows. An arrow:

f: A->B

Is a subset of a function spacef:{0}->B^A

fis called the 'name' of the function.

Classifier

In the opposite direction there is a correspondence between subsets of B and functions:

B->2

This is in the space 2^B which corresponds to the powerset(B), that is, all the possible subsets of B.

The characteristic arrow: xf classifies objects of B to determine if they are images of A. This is a pullback square. The object 2 has two values: 0 and 1. We also use the symbol Ω and call the elements 'true' and 'false'.

This means the topos theory is related to logic. (see also 'characteristic function' in number theory).

Predicate Category

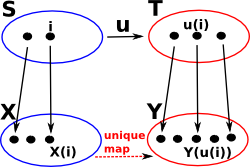
The relationship SX above is a predicate. We can form a category of predicates on sets as follows:

Objects	predicates are pairs (S,X) where SX X(i) implies an element iS is a free variable in S.
Morphisms	(S,X) -> (T,Y) where: u:S-> T and X(i) implies: Y(u(i))

See also - Predicate logic.

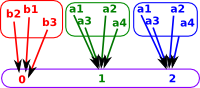
Family of Sets

A family of sets consists of an index set I and, for each element k of I, a set S_k.

There seems to be two ways to conceptulise this:

• As a 2-category. A set of sets.
• As disjoint sets.

Modest Sets

Set theoretic model of polymorphism.

Indexed Categories

(fibred category)

example

many sorted algebra ∑

Generalisation from Sets to Categories

Here we have illustrated some basic concepts using sets but they can be generalised to categories as shown here:

Sets	Categories
Injective Function No two distinct inputs give the same output. We can define 'A' a subset of 'B' by using an injective function from C	Monic Arrow Whenever f•g = f•h then g=h
Here we are showing this as an inclusion function because we are interested in subset classifiers. Injective function f: C >->B determines A as a subset of B (AB) Im f = {f(x): xC} where Im = Image Set inclusion is a partial odering on the Power set
Surjective function	Epic Arrow
Inverse Functions
Power Set	Power Object subobjects of d form a poset (Sub(d),)

see pages about:

• Topos Theory
• Topology
• HEP - Homotopy Extension Property
• Kan Extensions

HEP and Topos Theory

Relationship to homotopy extension principle.

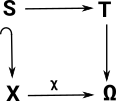
If we look at the category theory diagram for the homotopy extension principle HEP (see page here).
and then compare it to the above diagram for the sub-object classifier we can see that there is a similar thing going on: In the Topos case there may not be a requirement for continuous mappings but S is a subobject of X and the mapping between them is injective.

Topos Theory and Kan Extensions

Relationship to Kan extensions.

Again looking at the above diagram for the sub-object classifier:
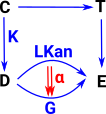
Compare it with the diagram for the Kan extension (see page here). The above diagram appears to be a special case of the Kan extension (most things are!) so, in this diagram, 'F' is a constant mapping and 'K' is injective.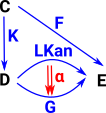
In order to make F constant we factor it through the terminal object. In the Topos case there may not be a requirement for continuous mappings but S is a subobject of X and the mapping between them is injective.

Topological Space

In many cases the concept of a metric space is unnecessary, however we still need the concept of 'nearness' and hence 'continuity'. 'Topological space' based on the 'topological open set' is the most general way we can do this. This allows us to define nearness purely using the concept of a subset.

Hausdorff Space

Hausdorff space is a bit more specific than general topological space. Space is Hausdorff if, in addition to being a topological open set, for any two points:
x₁, x₂X there are disjoint open sets U₁, U₂ that contain x₁and x₂.

Basis

A basis is a subcollection B= U

where

• U is the open set
• B is the basis
• = a subcollection (subset) - I need to add the proper symbol for this.

such that evey element of U is a union of open sets in B.

 

Computing Topos

https://github.com/fdilke/bewl

to install in openSUSE:

in YaST install:

• Scala
• SBT
• Git

on command line:

git clone https://github.com/fdilke/bewl.git
cd bewl
sbt console

EuclideanSpace

home

Prerequisites

See page here for a non-categorical approach to sub-objects.

Related Subjects

• Lattice - relation between logic and spaces
• Topological Space
• Category of Presheaves

Inverse Functions